| 28 展開図・投影図 (略解) | ||
| 28 展開図・投影図 (略解) | ||
| 1 | 東北学院高校 (R5年) ★ | 4 | 山形県立高校 (R5年) ★ | |||
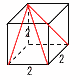 図は,ある立体図形の展開図です。この展開図を組み立ててできる立体の体積を求めなさい。 図は,ある立体図形の展開図です。この展開図を組み立ててできる立体の体積を求めなさい。【解】方錐(底面が正方形の四角錐) 底面は1辺2cmの正方形 高さは2cm 体積= |
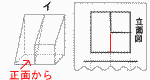 右の図は,投影図の一部である。この図から考えられる立体の見取図として適切でないものを,次のア~工から1つ選び,記号で答えなさい。 右の図は,投影図の一部である。この図から考えられる立体の見取図として適切でないものを,次のア~工から1つ選び,記号で答えなさい。【解】イ 左図の赤線が必要 |
|||||
| 2 | 青山学院高等部 (R7年) ★★ | 5 | 中央大附属高校 (R7年) ★ | |||
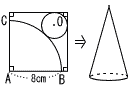 (1) 図のように,1辺が2cmの正四面体の展開図がある。この展開図を組み立てた四面体におけるACの長さと△ABCの面積を求めよ。点Cは辺の中点である。 (1) 図のように,1辺が2cmの正四面体の展開図がある。この展開図を組み立てた四面体におけるACの長さと△ABCの面積を求めよ。点Cは辺の中点である。【解】AC(1辺2の正三角形の高さ)= CM=√(√3)2-12= △ABC= 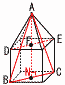 (2) 図のように,1辺が2cmの正方形と正三角形でできた九面体の展開図がある。この展開図を組み立てた九面体における△ABCの面積を求めよ。 (2) 図のように,1辺が2cmの正方形と正三角形でできた九面体の展開図がある。この展開図を組み立てた九面体における△ABCの面積を求めよ。【解】△ABCで,BC=2 △ABC= |
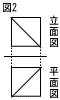 次の投影図において,曲線の部分は中心角が90°のおうぎ形の弧である。 次の投影図において,曲線の部分は中心角が90°のおうぎ形の弧である。(1) この立体の体積を求めなさい。 【解】四角柱-円柱× 体積=(8×15-82π× (2) この立体の表面積を求めなさい。 【解】底面積=8×15-82π× 側面積=(15+8+7+16π× 表面積=ア×2+イ=540+8π |
|||||
| 3 | 筑波大駒場附属高校 (R6年) ★★★ | 6 | 洛南高校 (R7年) ★★★ | |||
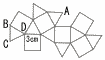 図は,ある立体Kの展開図です。立体Kのすべての面は正三角形または正方形であり,辺の長さはすべて3cmです。図のなかの4点A,B,C,Dは,それぞれ立体Kの頂点を表しています。 図は,ある立体Kの展開図です。立体Kのすべての面は正三角形または正方形であり,辺の長さはすべて3cmです。図のなかの4点A,B,C,Dは,それぞれ立体Kの頂点を表しています。この展開図を組み立ててできる立体Kについて, 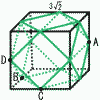 (1) 立体Kの体積を求めなさい。必要があれば,立方体の見取図を用いて考えなさい。 (1) 立体Kの体積を求めなさい。必要があれば,立方体の見取図を用いて考えなさい。【解】立方八面体(8つの角をカット) K=立方体-三角錐×8 =(3√2)3- (2) 線分ACの長さを求めなさい。 【解】△ACEで,AC2=CE2+EF2+AF2 =( 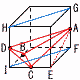 (3)三角すいA-BCDの体積を求めなさい。 【解】底面BCDに垂直な面HIFGで考える Aから△BCDへの垂線AJ(高さ)を求める △DKIで,DK={ √( 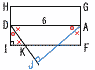 △ADJ∽△DKI(相似比 △ADJ∽△DKI(相似比AJ= 体積= |
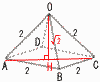 図のようにすべての辺の長さが2の正四角錐O-ABCDがあります。辺OB上を点Pが,辺OC上を点Qがそれぞれ動きます。辺CDの中点をMとします。 図のようにすべての辺の長さが2の正四角錐O-ABCDがあります。辺OB上を点Pが,辺OC上を点Qがそれぞれ動きます。辺CDの中点をMとします。(1) 正四角錐O-ABCDの体積を求めなさい。 【解】△OACで,OH= 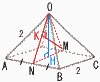 体積= 体積=(2) Mから△OABに下ろした垂線の長さを求めなさい。 【解】OM=ON= △OMN= 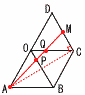 (3) 折れ線AP+PQ+QMの長さが最小になるとき, (3) 折れ線AP+PQ+QMの長さが最小になるとき,(ア) AP+PQ+QMの長さを求めなさい。 【解】展開図のAPQMが一直線のときで,∠ACM=60+30=90° △ACMで,APQM=√(2√3)2+12= (イ) 4点B,M,P,Qを頂点とする立体の体積を求めなさい。 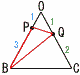 【解】OP= 【解】OP=
|
|||||