| 27 回転体 (略解) | ||
| 27 回転体 (略解) | ||
| 1 | 広島大附属高校 (R7年) ★ | 4 | 埼玉県立高校 (R6年) ★ | ||||||||||||||
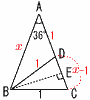 右の図のような直方体があります。三角形AEGを,対角線AGを軸として回転させたときにできる立体の体積を求めなさい。 右の図のような直方体があります。三角形AEGを,対角線AGを軸として回転させたときにできる立体の体積を求めなさい。【解】△AEGは等辺5の直角二等辺三角形 体積={ =(125/6) |
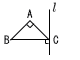
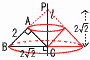 右の図のようなAB=AC=2cm,∠BAC=90°の△ABCがあり,頂点Cを通り,辺BCに垂直な直線/をひきます。このとき,△ABCを,直線/を軸として1回転させてできる立体の体積を求めなさい。 右の図のようなAB=AC=2cm,∠BAC=90°の△ABCがあり,頂点Cを通り,辺BCに垂直な直線/をひきます。このとき,△ABCを,直線/を軸として1回転させてできる立体の体積を求めなさい。【解】大円錐−小円錐×2 体積= |
||||||||||||||||
| 2 | 早大本庄高等学院 (R5年) ★★★ | 5 | 青雲高校 (R7年) ★★ | ||||||||||||||
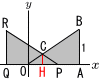 原点を0とする座標平面上に点A(√3,0), B(√3,1)がある。0≦t≦√3に対して,P(t,0), Q(t−√3,0), R(t−√3,1)をとる。直線PRと直線OBの交点をCとする。5つの線分で囲まれる部分の図形を,x軸を軸として一回転させてできる立体をMとする。 原点を0とする座標平面上に点A(√3,0), B(√3,1)がある。0≦t≦√3に対して,P(t,0), Q(t−√3,0), R(t−√3,1)をとる。直線PRと直線OBの交点をCとする。5つの線分で囲まれる部分の図形を,x軸を軸として一回転させてできる立体をMとする。(1) 点Cの座標をtを用いて表せ。 【解】 Cのx座標=(√3+t−√3)÷2=t/2 ∠AOB=30°より,Cのy座標=(t/2)× C(t/2, (2) 立体Mの体積Vをtを用いて表せ。 【解】円すい台( △COH∽△BOA(比t:2√3)で,体積比はt3:24√3
(3) 立体Mの表面積Sをtを用いて表せ。 【解】OB=2 S=
|
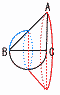 右の図は,∠Cを直角とする直角二等辺三角形ABCと辺BCを直径とする半円をつないだものであり,AC=BC=3cmである。この図形を直線BCを軸として1回転してできる立体の体積を求めよ。 右の図は,∠Cを直角とする直角二等辺三角形ABCと辺BCを直径とする半円をつないだものであり,AC=BC=3cmである。この図形を直線BCを軸として1回転してできる立体の体積を求めよ。【解】立体=半球+円すい台 体積= = |
||||||||||||||||
| 6 | 西大和学園高校 (R7年) ★★ | ||||||||||||||||
 図のような,一辺の長さが1の正六角形ABCDEFをAD を回転の軸として1回転してできる立体の体積は[あ ]である。また,BCを回転の軸として1回転してできる 立体の体積は[い ] である。ただし,円周率はπとして計算すること。 図のような,一辺の長さが1の正六角形ABCDEFをAD を回転の軸として1回転してできる立体の体積は[あ ]である。また,BCを回転の軸として1回転してできる 立体の体積は[い ] である。ただし,円周率はπとして計算すること。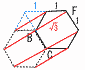 【解】BF= あ=円すい(高さ ={ い=円すい台(高さ ={ −{ = |
|||||||||||||||||
| 3 | 慶應義塾高校 (R5年) ★★★ | 6 | 市立堀川高校 (R6年) ★★ | ||||||||||||||
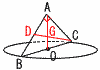 辺BC直径とする半径1の円0と辺BCを斜辺とする直角二等辺三角形ABCがある。 辺BC直径とする半径1の円0と辺BCを斜辺とする直角二等辺三角形ABCがある。(1) 通った部分の立体の体積を求めよ。 【解】Gは重心で,AG= (△ABOの回転体)−(△ADGの回転体)で, 体積= (2) 通った部分の立体の表面積を求めよ。 【解】(半径ACの半球)−(△ABCの回転体)で, 表面積=(半球の曲面積)+(円錐の側面積)
|
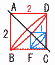 図のように,1辺の長さが2である正方形ABCDがある。辺ADの中点をE,辺BCの中点をFとする。 図のように,1辺の長さが2である正方形ABCDがある。辺ADの中点をE,辺BCの中点をFとする。(1) 正方形ABCDを,直線CDを回転の軸として1回転させたとき,四角形ABFEが通過してできる立体の体積を求めなさい。 【解】大円柱−小円柱 体積=(22−12)π×2=6π (2) 正方形ABCDを,直線ACを回転の軸として1回転させたとき,四角形ABFEが通過してできる立体の体積を求めなさい。 【解】赤円錐:青円錐=23:13=8:1 体積=(大円錐×2)× = |
||||||||||||||||