図形	２４　三角柱・三角すい　（略解）

１	岩手県立高校　（Ｒ４年）　★★★	５	慶応義塾志木高校　（Ｒ７年）　★★
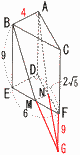図は,底面が直角三角形で,側面がすべて長方形の三角柱です。 (1) 線分BMの長さを求めなさい。 【解】△BEMで, 　BM＝\(\sqrt{9^2+3^2}\)＝√90＝3√10cm (2) 頂点D,Eをふくむ方の立体の体積 【解】(右上図参照) △ABCで,AB＝√62−(2√5)2＝4 (三角錐G-ABC)∽(三角錐G-NMF)で, 　相似比2:1だから,体積比は8:1 三角柱台ABC-NMF＝三角錐G-ABC× 　＝×(×4×2√5)×18×＝21√5…ア 三角柱ABC-DEF＝×4×2√5×9＝36√5…イ イ−アより, 体積＝15√5cm3		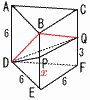図のように側面がすべて長方形であり,AB＝AC＝5, BC＝2, AD＝6である三角柱ABC-DEF がある。 また,点Mは辺BCの中点であり,点Pは辺AD上に,点Qは線分DM上にある.。AP＝4, ∠PQD = 90°であるとき, (1) 線分MQの長さを求めよ。 【解】△AMD∽△QPDより,6:QD＝2:2で,QD＝2/5√15 MQ＝MD−QD＝2−＝ (2) 三角錐Q-MEFの体積Vを求めよ。 【解】V＝(三角錐D-MEF)×(MQ/MD)＝4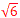×＝(16/5)
２	都立戸山高校　（Ｒ７年）　★★	６	日本大第二高校　（Ｒ５年）　★★
右の図に示した立体ABC-DEFは,AB＝10cm,AC＝ 5cm,AD＝28cm,∠BAC＝∠BAD＝∠CAD＝ 90°の三角柱である。点Pは辺AD上にある点で,AP＝xcm（0 ＜x＜28）,点Qは辺BE上にある点で,BQ＝15cmである。頂点Cと点P,点Pと点Q,点Qと頂点Cをそれぞれ結ぶ。 (1) △CPQが面BCFE と垂直になるとき,△CPQの面積は何cm2か。 【解】△ABCで,AG＝2　△QBCで,QC＝5 AG＝PHとなればよいから, △CPQ＝×5×2＝5√70cm2 (2) △CPQがPC＝PQの二等辺三角形になるとき,xの値を求めよ。 ただし,答えだけでなく,答えを求める過程が分かるように,途中の式や計算なども書け。 【解】△PACで,PC2＝x2＋52…ア △PQIで,QI＝x−15より,PQ2＝(x−15)2＋102…イ 　ア＝イより,x＝10 (3) 頂点Cと頂点D,頂点Dと点Qをそれぞれ結んだ場合を考える。立体D-CPQの体積が100cm3のとき,xの値を求めよ。 【解】(D-CPQ)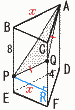＝△CDP×AB＝×(28−x)×10＝100 　(28−x)＝10より, x＝16		右の図のように,AD＝10cmの正三角柱ABC-DEFにおいて,BE上に点P,CF上に点Qを,それぞれEP＝2cm,FQ＝6cmとなるようにとると,∠AQP＝120°になった。 (1) ∠PAQの大きさを求めよ。 【解】 QP＝QAより,PAQ＝(180−120)÷2＝30° (2) 辺ABの長さを求めよ。 【解】AB＝xとおくと, △ABPで,AP＝\(\sqrt{x^2+64}\) △PQRで,QP＝\(\sqrt{x^2+16}\) (1)より,AP:QP＝2:2√3＝1:√3だから, 　\(\sqrt{x^2+64}\)：\(\sqrt{x^2+16}\)＝1:√3で, AB＝x＝2√2cm (3) この立体を平面APQで切断するとき,点Bを含む方の立体の体積を求めよ。 【解】 四角錐A-BPQC＝BPQC×高さ 　＝×(×12×2√2)×√6＝8√3ｃｍ3
４	秋田県立高校　（Ｒ６年）　★★★	７	都立八王子東高校　（Ｒ６年）　★★★
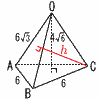
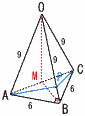右の図のように,三角錐OABCがある。点Aから辺OBを通り,点Cまで最も短くなるようにひいた線と辺OBの交点を Pとする。このとき,三角錐PABCの体積を求めなさい。 【解】ACの中点をMとすると,OM⊥△ABCで, 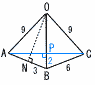　高さOM＝√92−(3√2)2＝3√7 △ONB∽△APB(相似比3:2)より,PB＝2 三角錐P-ABC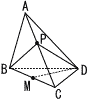＝(三角錐O-ABC) 　＝×(×62)×3√7×＝4√7cm3		立体Ａ-BCDは,AB＝AC＝BD＝CD,BC＝AD＝6cmの四面体である。BP＋PD＝lcmとする。 　点Ｐを辺AC上において動かすとき,最も小さくなるlの値を求めよ。 【解】 4面はすべて合同な二等辺三角形で底辺は6) △BCDで,DM＝4より,等辺BD＝AC＝5 △ABCに垂線BHを下ろし,AH＝xとすると, 　BH2＝52−x2＝62−(5−x)2より,x＝ 　BH＝, PH＝−＝で,BP＝√97 l＝2BP＝√97

［TOP］　［問題にもどる］　　★　中　　★★　やや難　　★★★　難