| 1 |
桜美林高校 (R7年) ★★ |
4 |
東海高校 (R7年) ★★★ |
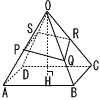 図のように,すべての辺の長さが12cmの正四角すいO-ABCDがある。辺OA上に点PをOP:PA=1:2となるようにとり,点B,C,Pを通る平面と辺ODとの交点をQとする。また,直線BPと直線CQとの交点をRとする。 図のように,すべての辺の長さが12cmの正四角すいO-ABCDがある。辺OA上に点PをOP:PA=1:2となるようにとり,点B,C,Pを通る平面と辺ODとの交点をQとする。また,直線BPと直線CQとの交点をRとする。
(1) 線分ORの長さを求めなさい。
【解】対称面四角OREFで考える
△ORM∽EFMで,OM:MEより,OR=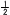 2EF=6cm 2EF=6cm
(2) 点Rと面ABCDとの距離を求めなさい。
【解】△OACで,OH=√OH2―AH2=√114−72=6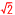 cm cm
(3) O,A,D,Rを頂点とする四面体OADRの体積を求めなさい。
【解】体積=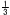 △ADR×OR= △ADR×OR=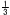 ×36 ×36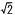 ×6=72 ×6=72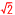 |
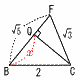 右の図のような長方形ABCDを底辺とする四角錐O-ABCDにおいて,AB=2cm,BC=4cm,OA=OB=OC=OD=3cmであり,辺OC,OD上の点P,QはPQ 右の図のような長方形ABCDを底辺とする四角錐O-ABCDにおいて,AB=2cm,BC=4cm,OA=OB=OC=OD=3cmであり,辺OC,OD上の点P,QはPQ CDを満たしている。 CDを満たしている。
(1) 四角錐O-ABCDの体積は[ ]cm3である。
【解】△OBHで,OH=√32−(√5)2=2
体積V=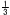 ×(2×4)×2= ×(2×4)×2=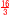
(2) 四角錐O-ABPQの体積が四角錐O-ABCDの体積のちょうど半分であるとき,OP=[ ]cmである。 
【解】四角錐O-ABCD=(三角錐O-ABQ)+(三角錐O-CBQ)
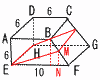 (1×1× (1×1×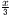 )+ )+ (1× (1×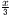 × ×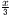 )= )=
x2+3x−9=0(0<x<3)より, OP= (3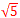 −3)/2 −3)/2 |
| 2 |
秋田県立高校 (R5年) ★★ |
5 |
愛知県立高校 (R7年) ★★★ |
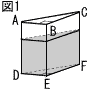 図1のように,三角柱ABC-DEFの形をした透明な容器に,水を入れて密閉した。この容器の側面はすべて長方形で,AB=6cm,BC=8cm,CF=12cm,∠ABC=90°である。 図1のように,三角柱ABC-DEFの形をした透明な容器に,水を入れて密閉した。この容器の側面はすべて長方形で,AB=6cm,BC=8cm,CF=12cm,∠ABC=90°である。
図2のように,四角形FEBCが容器の底になるように,水平な台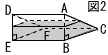 の上に置きかえたとき,容器の底から水面までの高さを求めなさい。 の上に置きかえたとき,容器の底から水面までの高さを求めなさい。
【解】(右下図参照)
| 図1で, |
水 の 容積 |
= |
水 の 高さ |
= |
8 |
= |
 |
| 容器の体積 |
容器の高さ |
12 |
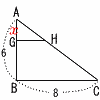 図2の△ABCで,AG=xとすると, 図2の△ABCで,AG=xとすると,
体積比より,次のようになればよい
△AGH:△ABC=x2:62=1:3
x2=36÷3=12で,x=2√3
GB=(6−2√3)cm
|
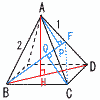 図で,立体OABCDは,正方形ABCDを底面とする正四角すいである。また,E,F,G,Hはそれぞれ辺OA,OB,OC,OD上の点で,OE:EA=2:1,OF:FB=1:1
であり,CB 図で,立体OABCDは,正方形ABCDを底面とする正四角すいである。また,E,F,G,Hはそれぞれ辺OA,OB,OC,OD上の点で,OE:EA=2:1,OF:FB=1:1
であり,CB GF,DA GF,DA HEである。OA=12cm,AB=6cmのとき, HEである。OA=12cm,AB=6cmのとき,
(1) △OBDの面積は[ ]cm2である。
【解】△OBMで,OH=√122−(3√2)2=3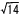
△OBD=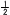 ×6 ×6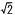 ×3 ×3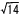 =18 =18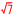 cm2 cm2
(2) 立体OEFGHの体積は[ ]cm3である。
【解】IJ=3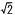 × ×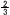 +3 +3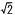 × ×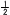 = = 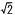
体積=三角錐(E-OFH)+三角錐(G-OFH)=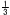 △OEF×IJ △OEF×IJ
=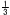 ×6 ×6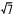 ×7/2 ×7/2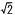 =7 =7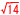 cm3 cm3 |
| 3 |
桐朋高校 (R6年) ★★★ |
6 |
法政大国際高校 (R6年) ★★★ |
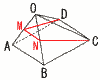 AB=1である長方形ABCDを底面とする四角錐O-ABCDで, AB=1である長方形ABCDを底面とする四角錐O-ABCDで,
(1) △OBCの面積を求めよ。
【解】OB=OC=AD=√2で,△OBCは正三角形
△OBC=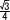 ×(√2)2= ×(√2)2=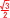
(2) 四角錐O-ABCDの体積を求めよ。
【解】∠OAB=∠DAB=90°より,高さ=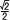
体積=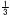 ×(1×√2)× ×(1×√2)×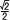 = =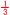
(3) このとき,点Oを含む方の立体の体積を求めよ。
【解】MN⊥△OAD
△OMDを底面とする切頭三角柱と考える
△OMD=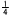 , MN= , MN=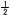 ,DC=1より, ,DC=1より,
| 体積=底面積×高さの平均= |
1 |
× |
0+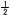 +1 +1 |
= |
1 |
| 4 |
3 |
8 |
|
 (1) 四角錐A-BCDEの表面積を求めよ。 (1) 四角錐A-BCDEの表面積を求めよ。
【解】側面の高さ=√122−32=3√15
表面積=(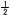 ×6×3√15)×4+62=36(√15+1) ×6×3√15)×4+62=36(√15+1)
(2) 四角錐A-BCDEの体積を求めよ。
【解】△ABDの高さ=√ { 122−(3√2)2}=3√14
 体積= 体積=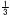 ×62×3√14=36√14 ×62×3√14=36√14
(3) このとき,四角形PQRSの面積を求めよ。
【解】 PQRSは等脚台形 PQRSは等脚台形
△PQKで,PK=3√15×(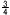 − −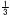 )= )=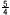 √15, √15,
QK=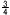 +2= +2=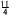
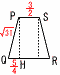 PQ=√ { ( PQ=√ { (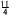 )2+( )2+(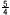 √15)2}=√31 √15)2}=√31
△PQHで,PH=√ { (√31)2−(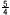 )2}= )2}=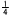 √471 √471
 PQRS= PQRS=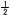 ×( ×(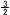 +4)× +4)×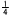 √471=(11/16)√471 √471=(11/16)√471 |