図形	１８　作　図　（略解）
以下の問題では,定規とコンパスを用いて作図し,作図に用いた線は消さないでおくこと。

１	お茶の水女子大附属高校　（Ｒ５年）　★★★	４	早稲田実業高等部　（Ｒ７年）　★★
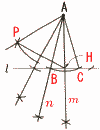
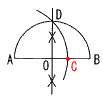
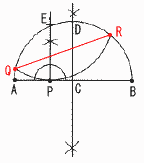
∠A＝30°,AB＝ACである二等辺三角形ABCで辺BCが直線l 上にあるものを作図せよ。		図のように長さ２の線分ＡＢがある。このとき,点Ａを中心とする半径の円を作図せよ。
・Aからl に垂線mを引く ・正三角形APHを作図する ・∠PAHの4等分を考え,直線nを引く ・l とnの交点をBとする ・AB＝ACとなるように,l上にCをとる ・3点A,B,Cを結ぶ		〜△MCB（30°60°90°の直角三角形)を作図する〜 ・BからABの垂線l を引く ・ABの中点Mをとる ・l 上にAB＝BCとなる点Cをとる ・Aを中心に,半径ACの円をかく
２	都立日比谷高校　（Ｒ７年）　★★	５	慶応義塾志木 高校　（Ｒ７年）　★★
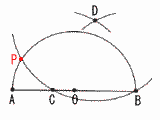
図で,点Pは△ABC の外部にある点で,∠ACB ＝∠APB,∠ABP＝90°である。 　解答欄に示した図をもとにして,点Pを1つ,作図によって求め,点Pの位置を示す文字Pも書け		y軸上に原点Oと異なる点Pがあり,直線y＝2x上に点Qがある。点Pを通り,点Qで直線y＝2xと接する円をCとする。 　図のように点P,Qがあるとき,円Cを作図せよ。
〜△ABCの外接円を作図する〜 ・ABの垂直二等分線l とBCの垂直二等分線mの交点O(外心)をとる ・AOを延長して,外接円との交点をPとする		・PQの垂直二等分線l を引く ・Qから直線y＝2xの垂線mを引く ・l とmの交点Cとし,Cを中心に半径CPまたはCQの円をかく
３	県立膳所高校　（Ｒ６年）　★★	６	都立立川高校　（Ｒ６年）　★★★
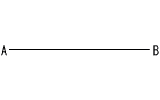
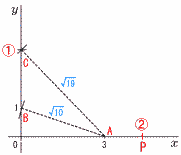
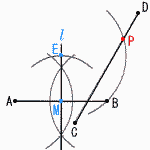
図の座標平面のx軸,y軸上にそれぞれ点(3,0),点(0,1)が与えられている。 解答用紙にある座標平面のx軸上に,点Ｐ(√19, 0)を作図しなさい。		図のように,線分ABと線分CDがあり,互いに文わっている。 　図をもとにして,線分CD上にあり∠APB＝45°となる点Pを,定規とコンパスを用いて作図し,点Pの位置を示す文字Pも書け。
・AB＝OC(長さ√10)となる点Cをとる ・AC＝OP(長さ√19)となる点Pをとる		・ABの垂直二等分線l上に,AM＝EMとなる点Eをとる ・直線CD上に,EB＝EPとなる点Pをとる

［TOP］　［問題にもどる］　　★　中　　★★　やや難　　★★★　難