 図形 |
１４ 平行四辺形 （略解） | |
| 図形 |
１４ 平行四辺形 （略解） | |
| １ | 和歌山県立高校 （Ｒ５年） ★ | ５ | 城北高校 （Ｒ６年） ★★ |
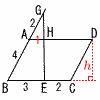 平行四辺形ABCDの辺BC上に点Eがある。 図のように,AB＝4cm,BE＝3cm,EC＝2cmのとき,辺BAの延長上にAG＝2cmとなるように点Gをとる。また,GEとADの交点をHとする。 このとき,台形ABEHの面積は,平行四辺形ABCDの面積の何倍になるか,求めなさい。 【解】  ABCDの高さをhとする△GAH∽△GBE(比1:3)より,AH＝1 台形ABEH÷ ABCD＝ (1＋3)h÷5h＝2h÷5h＝ 倍 |
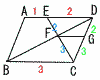 右の図の平行四辺形ＡBCDにおいて,辺AD上に点Eをとり,BDとCEの交点をＦとする。また,辺CD上にFG‖ＢBCとなるような点Gをとる。AE:ED＝1:2のとき,△DFGと△FBCの面積比を求めよ。【解】△FDE∽△FBC(相似比2:3) DG:DC＝2:5より,△DFG:△DBC＝22：52＝4:25 また,△DFG:△CFG＝2:3だから, △DFG:△FBC＝4:(25−4−6)＝4:15 |
||
| ２ | 東京科学大附属科技高校 （Ｒ７年） ★ | ６ | 日大第三高校 （Ｒ７年） ★★ |
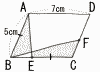 図のようにAB＝5cm,AD＝7ｃｍである平行四辺形ABCDがある。点E,Fはそれぞれ辺BC,CD上の点であり,AB＝CEである。影をつけた2つの部分の面積が等しいとき,線分CFの長さを求めなさい。【解】AB  FC△ABE＝△FBCより,2×5＝7CFになればよい CF＝10/7cm |
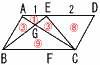 右の平行四辺形ABCDにおいて,AE＝ED,BF＝FG＝GCである。対角線BD上の,EF,EGと交わる点をそれぞれH,Ｉ とするとき,BH：H
I：I Dをもっとも簡単な整数の比で表しなさい。【解】AD＝BC＝6とすると, △BFH∽△DEHより,BH:HD＝2:3＝14:21…ア △BGI ∽△DEI より,BI :I D＝4:3＝20:15…イ アイより, BH：H I：I D＝14:(20−14):15＝14:6:15  |
||
| ３ | 専修大附属高校 （Ｒ５年） ★ | ７ | 鹿児島育英館高校 （Ｒ６年） ★★ |
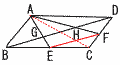 平行四辺形ABCDの面積を１とするとき,(1) AG:GEを求めなさい。 【解】Gは△ABCの重心で,AG:GE＝2:1 (2) △ABGの面積を求めなさい。 【解】△ABG＝  △ABE＝×△ABC＝ ××ABCD＝ ABCD＝ (3) △AEFの面積を求めなさい。 【解】△ABE＝△ADF＝  , △CEF＝×＝ △AEF＝1−( ＋＋)＝ |
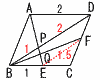 ABCDにおいて,辺BC,CDの中点をそれぞれE,Fとし,線分AEとBD,BFとの交点をそれぞれP,Qとする。(1) AP:PQ:QEを求めよ。 【解】△PAD∽PEB(相似比2:1)で,AP:PE＝2:1…ア BP＝  BD, EF＝BDで, BP：FE＝2:3△QPB∽△QEF(相似比2:3)より,PQ:QE＝2:3…イ アイより,AP:PQ:QE＝10:2:3 (2) ABCDの面積は△PBQの面積の何倍か求めよ。【解】(1)より,PQ＝  AEABCD＝4△ABE＝4× △PBQで, 30倍 |
||
| ４ | 盈進高校 （Ｒ７年） ★ | ８ | 青山学院高等部 （Ｒ７年） ★★ |
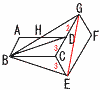 次の図のように,AB＝3cm,BC＝5cm,∠ABC＝60°である平行四辺形ABCDがある。平行四辺形ABCDと四角形CEFGは合同な図形である。また,辺CG上に点Dがあり,辺BGと辺ADとの交点をHとする。（1）この図において,三角形BCDと合同な三角形をすべて答えなさい。 【解】△DAB, △BCE （2）平行四辺形ABCDの面積をSとするとき,三角形BCGの面積をSを用いて表しなさい。 【解】△BCD＝3kとすると,S＝平四ABCD＝3k×2＝6k △BCG＝3k＋2k＝5k＝  △BCD＝ S（3）四角形BEFGの面碩は,平行四辺形ABCDの面積の何倍であるか求めなさい。 【解】）四BEFG＝△BCG＋△BCE＋  CEFG＝5k＋3k＋6k＝14kABCD＝S＝6kだから, 14k÷6k＝ 倍 |
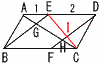 図のように,平行四辺形ABCDがあり,辺ADを2：1 に分ける点をE,辺CDを2:3に分ける点をF,Eを通り辺ABと平行な直線と辺BCとの交点をG,直線EGと直線AF,BFの交点をそれぞれP,Qとする。このとき,次の比を求めよ。ただし,最も簡単な整数の比で表すこと。(1) EP：PG 【解】EP＝3×  ＝2, PQ＝5× ＝ , QG＝2×＝ EP：PG＝2：( ＋)＝2:3(2) EP：PQ：QG 【解】(1)より,EP：PQ：QG＝2: :＝6：5：4(3) 四角形ABQPの面積をS1,四角形EPFDの面積をS2としたとき,S1：S2 【解】ともに上底下底が平行な台形 S1：S2＝{( ＋5)×2}：{(2＋3)×1}＝(40/3)：5＝8:3 |
||