図形	４　三平方の定理　（略解）

１	東海大付属浦安高校　（Ｒ５年）　★	６	江戸川学園取手高校　（Ｒ５年）　★★
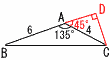△ABCの面積は(　　)になります。 【解】（右図参照） △DACは直角二等辺三角形だから, 　CD:4＝1:√2で,CD＝4/√2＝2√2 よって, △ABC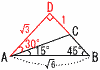＝×6×2√2＝6√2		辺BCの長さを求めなさい。 【解】（右図参照） △DABは直角二等辺三角形だから, 　DA:√6＝1:√2で,DA＝DB＝√3 また,DC＝1より, BC＝√3−1
２	玉川学園高等部　（Ｒ７年）　★	７	近畿大附属高校　（Ｒ４年）　★★★
∠C＝90°,AB＝c,BC＝a,CA＝bの直角三角形ABCにおいて,∠Aに着目したとき,XA,YA,ZAという記号を次のように定める。 　XA＝, YA＝, ZA＝　　　 (1) ∠Ｃ＝90°の直角三角形ABCにおいて,YA＝のとき, ZAの値を求めよ。 【解】a＝で,ZA＝/2 (2) ∠Ｃ=90°の直角三角形ABCにおいて,5(XA)2十(YA)2−4XA＝Oのとき,XAの値と∠Ａの大きさを求めよ。 【解】5()2十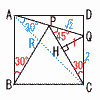()2−4＝Oより,(2aーc)2＝0で,c＝2a XA＝＝a/2a＝		(1) ∠PABの大きさを求めよ。 【解】△ABPで∠B＝30°, BA＝BP 　∠PAB＝(180−30)÷2＝75° (2) 辺BCの長さを求めよ。 【解】∠QPH＝180−75−60＝45°で, 　△QPHは,45,45,90°で,PH＝QH＝1…ア △CQHは,30,60,90°で,CH＝√3 …イ ア＋イより, BC＝PC＝1＋√3 (3) 線分APの長さを求めよ。 【解】△ADQで,AQ2＝(1＋√3)2＋(1＋√3−2)2＝8 よって, AP＝2√2−√2＝√2 (4) 線分PRの長さを求めよ。 【解】△APR∽△BAP(2角相等)より, PR＝√2× 　√2 . ＝√3−1 √3＋1 (5) △PRCの面積を求めよ。 【解】(2)より,AC＝√2(√3＋1)＝√6＋√2 　CR＝AC−AR＝√6＋√2−√2＝√6 △PRC＝△ACQ× AP × CR ＝(√3＋1)×× 　√6　. ＝ √3 AQ AC √6＋√2 2
３	早大本庄高等学院　（Ｒ７年）　★★
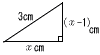下図の四角形ABCDに対し,線分BD上の点E,FをそれぞれAE⊥BD,CF上BDとなるようにとる。線分EFの長さを求めよ。 【解】BD＝BE＋ED＝6＋3＝9 △BCDで,BF＝xとすると,CF2＝41−x2＝50−(9−x)2 　x＝4で, EF＝6−4＝2
４	明治学院高校　（Ｒ６年）　★	８	立教新座高校　（Ｒ６年）　★★
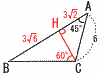図のような△ABCの面積を求めよ。 【解】垂線CHをおろす △ACHで,AH＝CH＝6/√2＝3√2 △BCHで,BH＝√3CH＝3√6 △ABC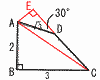＝×(3√2＋3√6)×3√2＝9＋9√3		図の四角形の面積を求めなさい。 【解】∠ADE＝30° △ADEで,AE＝,DE＝　　CE＝ ABCD＝△ABC＋(△ACE−△ADE) 　＝3＋(√3−√3)＝3＋cm2
５	鎌倉学園高校　（Ｒ６年）　★★★	９	専修大付属高校　（Ｒ６年）　★★
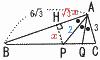直角三角形ABCがあります。 (1) 点Pから辺ABへ垂線PHを下ろすとき,PH の長さを求めなさい。 【解】PH＝xとすると,BH＝6√3−√3x…ア HP‖ACで,BH＝6√3×(x/3)＝2√3x…イ ア＝イより,6√3−√3x＝2√3xで,x＝PH＝2 (2) BPの長さを求めなさい。 【解】 △BPHで,BP2＝22＋(4√3)2より, BP＝2√13 (3) △APQの面積を求めなさい。 【解】BC＝3√13より,PC＝√13で,PQ＝PC＝√13 △APQ＝△ABC×(PQ/BC)＝9√3×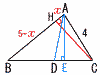＝√3		AB＝5,BC＝6,CA＝4である。 (1) AHの長さを求めなさい。 【解】AH＝x,BH＝5−xとすると, CH2＝42−x2＝62−(5−x)2で,x＝AH＝ (2) △ABCの面積を求めなさい。 【解】CH2＝42−()2より,CH＝√7 △ABC＝×5×√7＝√7 (3) ADの長さを求めなさい。 【解】(2)より,垂線AE＝√7÷3＝√7 △ABEで,BE2＝52−(√7)2より,BE＝ BD＝BC＝だから, DE＝−＝ △ADEで,AD2＝(√7)2＋()2＝100/9より, AD＝

［TOP］　［問題にもどる］　　★　中　　★★　やや難　　★★★　難