| 1 合同な図形 (略解) | ||
| 1 | 新潟県立高校 (R5年) ★ | 5 | 埼玉県立高校 (R5年) ★★ | |||||||||||
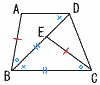 AB=ECであることを証明しなさい。 AB=ECであることを証明しなさい。【証明】△ABDと△ECBで,
よって, AB=EC |
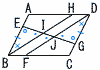 △BEI≡△DGJであることを証明しなさい。 △BEI≡△DGJであることを証明しなさい。【証明】 △BEIと△DGJで,
|
|||||||||||||
| 2 | 大阪教育大平野校舎高校 (R6年) ★★ | 6 | 高知県立高校 (R6年) ★ | |||||||||||
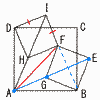 右の図において,四角形ABDD,BEFG,DHFI はすべて正方形である。それぞれの正方形は,図のように2点を他の正方形と共有している。3点A,H,Iが同一直線上にあるとき, 右の図において,四角形ABDD,BEFG,DHFI はすべて正方形である。それぞれの正方形は,図のように2点を他の正方形と共有している。3点A,H,Iが同一直線上にあるとき,(1) AD=AFを証明しなさい。 【証明】△ADI と△AFI で,
(2) 3点A,G,Eが同一線上にあることを示しなさい。 【証明】
|
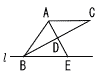
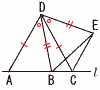 右の図のように,直線l上に3点A,B,Cをとり,辺ACを一辺とする正三角形ACDと,辺DBを一辺とする正三角形BEDをつくり,点Cと点Eを結ぶ。 右の図のように,直線l上に3点A,B,Cをとり,辺ACを一辺とする正三角形ACDと,辺DBを一辺とする正三角形BEDをつくり,点Cと点Eを結ぶ。(1) △ABD≡△CEDを証明しなさい。 【証明】△ABDと△CEDで,
(2) AD=4cmのとき,四角形BCEDの面積を求めなさい。 【解】(1)より,△ABD=△CED 四角形BCED=△BDC+△CED=△BDC+△ABD=△ACD = |
|||||||||||||
| 3 | 広島県立高校 (R6年) ★ | 7 | 東京電機大高校 (R7年) ★★ | |||||||||||
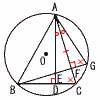 △ABCは鋭角三角形で,頂点A,B,Cは円Oの円周上にあります。△AEF≡△AGFであることを証明しなさい。 △ABCは鋭角三角形で,頂点A,B,Cは円Oの円周上にあります。△AEF≡△AGFであることを証明しなさい。【証明】∠ACD=∠AGF( △AEFと△AGFで,
|
 図において,△ABCと△ADEは正三角形で,∠ADB=75°,AE= 図において,△ABCと△ADEは正三角形で,∠ADB=75°,AE=(1) ∠CAEの大きさを求めなさい。 【解】△ABDで,∠BAD=180−60−75=45° ∠CAE=∠BAD=45° (2) ∠AECの大きさを求めなさい。 【解】△ABD≡△ACE(2辺夾角相等)より,∠AEC=∠ADB=75° (3) 辺ABの長さを求めなさい。 【解】△ADHで,AH=DH=2 △BDHで,BH= AB=AH+BH=2+ (4) 四角形ABCEの面積を求めなさい。 【解】△ABC= △ACE=△ABD= ア+イより, |
|||||||||||||
| 4 | 西大和学園高校 (R6年) ★★ | |||||||||||||
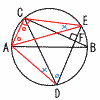 三角形CAEと三角形ACDが合同であることを証明せよ。 三角形CAEと三角形ACDが合同であることを証明せよ。【証明】∠ACB=90°(直径の円周角),BC⊥DE AC‖DEとなるから,∠ACD=∠EDC(錯角)…ア ∠ECD=∠CAE( △CAEと△ACDで,
|
||||||||||||||
[TOP] [問題にもどる] ★ 中 ★★ やや難 ★★★ 難