 関数 |
２８ 座標平面３ （略解） | |
| 関数 |
２８ 座標平面３ （略解） | |
| １ | 和歌山県立高校 （Ｒ５年） ★★ | ４ | 明治大明治高校 （Ｒ７年） ★★★ | ||
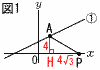 図１のように,関数y＝ x＋3…① のグラ フ上に点A(2,4)があり,x軸上に点Pがある。 (1) ∠APO＝30°のとき,Pのx座標を求めなさい。 【解】垂線AHをおろすと,HP＝4√3 x＝2＋4√3 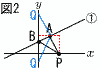 (2) 図2のように,①のグラフとy軸との交点をBとする。また,y軸上に点Qをとり,△ABPと△ABQの面積が等しくなるようにする。Pのx座標が4のとき,Qの座標をすべて求めなさい。【解】△ABP＝正方形－3つの直角三角形 △ABP＝4×4－(6＋4＋1)＝16－11＝5 △ABQ＝ BQ×2＝5より,BQ＝5になればよい。3－5＝－2で, Q(0,－2) 3＋5＝8で, Q(0,8) |
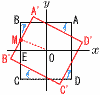 p＞０とする。Oを原点とする座標平面上に,4点Ａ(3 ,p),B(－3, p),C(－3,－p),D((3,－p)を頂点とする長方形ＡBCDがある。この長方形ＡBCDを,点Oを中心として反時計回りに60°だけ回転移動させた。4点A,B,C,Dの移動後の点をそれぞれA'B'C'D'とすると,辺Ａ'B'の中点は辺BC上の点となった。(1) pの値を求めよ。 【解】△OME(30°60°90°)で,OM＝p,OE＝3 OM:OE＝p: 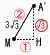＝2:より, p＝6 (2) 点Ａ'の座標を求めよ。【解】M(－3 ,3),A'Mの傾きは,A'M＝3△A'MH(1:2: )より, A'(－  , )(3) 長方形ABCDと長方形A'B'C'D'が重なる部分の面積を求めよ。 【解】ア＝  ××3＝ イ＝×3×3＝  ABCD－ア－イ＝72－－＝60 |
||||
| ２ | 千葉県立高校 （Ｒ７年） ★★ | ５ | 筑波大附属高校 （Ｒ６年） ★★★ | ||
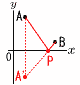 下の図のように,関数y＝x2のグラフ上に2点A,Bがあり,座標はそれぞれ2.4である。 y軸上に点PをAP＋BPの長さが最も短くなるようにとり,x軸上に点QをAP＋BP＝BQ となるようにとるとき,点Qとして考えられる2点を,Q1, Q2とすると,線分Q1Q2の長さは[ ]cmである。 ただし,原点から点(1,0)までの距離及び原点から点(0,1)までの距離をそれぞれ1cmとする。 【解】Aのy軸対称点A'（－2,2)をとると, AP＋BP＝BA'＝BQ＝6  二等辺三角形BQ1Q2で,等辺6 ,高さ8より,底辺Q1Q2＝4 |
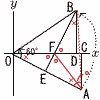 座標平面の点Ａ(8,－4)を,原点Oを中心として反時計回りに60゜だけ回転させた点をＢとし,その座標を以下のような方法で求めることを考える。2点A,Bからx軸に垂線AC,BDを引く。また,点Bから線分OAに引いた垂線BEとx軸との交点をＦとする。 (1) 線分OEの長さは,[ ]である。 【解】OA＝√82＋(－4)2＝4√5 △OABは正三角形だから,OE＝ OA＝2√5(2) 7点O,A,B,C,D,E,Fから3点を選んでつくる三角形のうち,△OACと相似な三角形は△OAC以外に3つあり,[ ],[ ],△AFEである。 【解】二角相等より,△OFE,△BFD (3) 線分BFの長さは,[ ]である。 【解】△OAC∽△OFE（比√5:2:1)より, OE＝2√5で,EF＝2√5× ＝√5△OEBで,BE＝2√5×√3＝2√15より, BF＝2√15－√5 (4) 点Bの座標は( [ ], [ ] )である。 【解】 EF＝√5で,△OAC∽△OFEより,OF＝√5×√5＝5 FD＝(2√15－√5)×(1/√5)＝2√3－1 BD＝2FD＝4√3－2で, B(2√3＋4, 4√3－2) |
||||
| ３ | 明大付属八王子高校 （Ｒ６年） ★★ | ||||
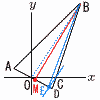 右の図のように,3点A(－2,2),B(6,18),C(3,0)があります。直線AOと直線BCの交点をDとします。(1) 点Bを通り,△ABDの面稿を2等分する直線の式を求めなさい。 【解】AOはy＝－x…ア,BCはy＝6x－18…イ アイの交点は,－x＝6x－18より,D(  ,－)2等分線はBとADの中点M(  ,－)を通るから,
(2) 辺AD上に点Eをとります｡△ABEと四角形OABCの面積が等しくなるような点Eの座標を求めなさい。 【解】BOの平行線CEは,y＝3(x－3)＝3x－9…ウ ア＝ウより,－x＝3x－9で,交点E(  ,) |
|||||
x－