 関 数 |
２５ 放物線と四角形２ （略解） | |
| 関 数 |
２５ 放物線と四角形２ （略解） | |
| １ | 大阪産大附属高校 （Ｒ７年） ★ | ４ | 江戸川学園取手高校 （Ｒ７年） ★★★ | ||||
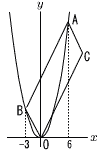 図のように,2つの放物線y＝ x2…①,y＝x2…②があります。放物線①上に点Ａをとり,点Ａのx座標をaとします。点Ａを通りx軸に平行な直線と,放物線②との交点をB,点Bを通りy軸に平行な直線と,放物線①との交点をC,線分AB,BCを2辺とする長方形をABCDとします。⑴ a＝6のとき,点Ａの座標を求めなさい。 【解】①にx＝6を代入して, A(6,9) (2) ⑴のとき点Bの座標を求めなさい。 【解】②にy＝9を代入して, B(3,9) (3) 点Cの座標をaを用いて表しなさい。 【解】B(  a,a2)より, C( a, a2)(4) 長方形ABCDが正方形となるとき,点Aのx座標aを求めなさい。 【解】AB＝a－ a＝a AD＝a2－ a2＝ a2a＝3/16a2より, a＝ |
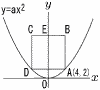 右の図のように2つの放物線y＝x2,y＝ax2が直線y＝xとそれぞれ原点Oと異なる2点Ａ,Bで交わっている。この2点A,Bをy軸に関して対称に移動した点をそれぞれD,Cとする。ただし,aは正の定数とする。(4)は途中過程も記述しなさい。(1) a＝  のとき点Bの座標を求めなさい。【解】 x2＝xより,x＝ で, B( ,)(2) OA:OB＝1:2のとき,aの値を求めなさい。 【解】x2＝xより,A(1,1)で,OA:OB＝1:2だからB(2,2) これをy＝ax2に代入して,22a＝2より, a＝ |
||||||
| ２ | 大阪星光学院高校 （Ｒ５年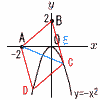） ★★★ |  以下ではOA:OB＝1:2として,台形ＡBCDを,点Aを中心として時計回りに135°回転させる。このとき,点B,C,Dが移動した点をそれぞれB',C',D'とする。(3) 点C'の座標を求めなさい。 【解】(右図参照) AB'＝AB＝  B'C'＝BC＝4より,B'H＝C'H＝2 C'のx座標は1＋2 C'のy座標は1－＋2＝1＋よって, C'(1＋2  ,1＋) (4) 台形AB'C'D'を,x軸のまわりに１回転させてできる立体の体積を求めなさい。【解】(右図参照) (1＋)2π－ ･12π＝(3＋4)π＋π＝(3 ＋ )π |
|||||
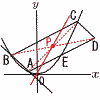 放物線y＝ x2と直線y＝－2x－ が2点A,Bで交わっている。(1) 点Aのx座標は( ), 点Bのx座標は( ) 【解】 x2＝－2x－より,x2＋4x＋3＝0これを解いて, 点Aは－1, 点Bは－3 (2) 点Eのx座標をtで表すと( )となり,したがってt＝( ) 【解】A(－1, ) B(－3, )で, E(e,e2)とすると,
A,B,Cの位置関係より,D(t＋2, t2－4)Eは中点だから, (t＋2)＋(－1)＝2(t－2)で, t＝5 (3) 原点Oを通り,  ABCDを二等分する直線の式はy＝( )【解】対角線の交点,つまりAとCの中点Pを通る C(5,  )より,P(2, )となって, y＝ x |
|||||||
| ３ | 慶應義塾女子高校 （Ｒ６年） ★★ | ５ | 早大高等学院 （Ｒ６年） ★★★ | ||||
放物線y＝x2上に3点Ａ(－2,4),B(b,b2),C(c,c2)があり,原点を通り四角形OABCの面積を２等分する直線を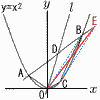 l ,直線ABと直線l の交点をDとする。直線ABの傾きは2で,直線l の式がy＝ xのとき,(1) bの値を求めなさい。 【解】ABはy＝2(x＋2)＋4＝2x＋8で,これにBを代入して, b2＝2b＋8より, b＝4 (2) ,△OAD＝△ODEとなるような点Eのx座標 【解】2x＋8＝ xより,D(,11)AD＝DEより,Eのx座標は,x＝ ＋(＋2)＝5(3) cの値として考えられるものをすべて答えなさい。 【解】  ODBC＝△ODE＝OABCとなればよいつまり,CE∥OBで,B(4,16)より,CEはy＝4(x－5)＋18＝4x－2 x2＝4x－2を解いて,x＝c＝2±√2 |
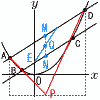 (1) 直線BCの傾きとy切片【解】B(－1,a),C(3,9a)
【解】A(－2,4a) ADはy＝2a(x＋2)＋4a＝2ax＋8a…イ ア＝イより,ax2＝2ax＋8aで,これを解いて, x＝4 (3) 四角形ABCDの面積をaの式で表せ。 ABはy＝－3ax－2a…ウ DCはy＝7ax－12a…エ 交点Pはウ＝エより, P(1,－5a)で,△PAD＝45a △PBC∽△PAD(比2:3)より, ABCD＝ △PAD＝25a(4) ABCDのを2等分するものの傾きをaの式で表せ。 【解】ADの中点M(1,10a),BCの中点N(1,5a) MNの中点Q(1,  a)とE(0,3a)を通ればよいから,2等分線の傾き＝( a－3a)÷1＝ a |
||||||