関数	２２　放物線と円　（略解）

１	洛南高校　（Ｒ５年）　★★★	４	城北高校　（Ｒ７年）　★★★
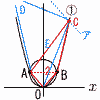(1) aの値を求めなさい。 【解】B(2,2)を①に代入して, 2＝22aで, a＝ (2) Cの座標を求めなさい。 【解】底辺ABが共通,高さも8倍 Cのy座標＝2×8＋2＝18で, 　18＝x2より, C(6,18) (3) Dの座標を求めなさい。 【解】底辺OAが共通だから,平行線アを引く y＝－(x－6)＋18＝－x＋24 …ア x2＝－x＋24で,x2＋2x－48＝0より, D(－8,32) (4) 四角形OCDAの面積を求めなさい。 【解】ACはy＝2x＋6 △OCA＝OE×(CとAのx座標差)＝×6×(6＋2)＝24…イ ACが共通で,△OCA:△ACD＝OA:CD 　＝(OとAのx座標差):(CとDのx座標差)＝1:7 　△ACD＝7△OCA＝7×24＝168…ウ イ＋ウより, 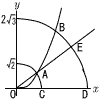OCDA＝24＋168＝192		右の図のように放物線y＝x2上に中心があり,半径がである２つの円がある。一方の円の中心は原点Oで,もう一方の円の中心を点Ａとし,点Ａのx座標は正とする。この２つの円が点Bで佞しているとき, (1) 点Ａのy座標をt として,t の値を求めよ。 【解】A(√t ,t)より,OA2＝t＋t2＝(×2)2＝6 t2＋t－6＝(t＋3)(t－2)＝0より, t＝2 (2) 点Bで２つの円に接する直線の式を求めよ。 【解】OAと垂直だから,傾きは－ B(,1)より,y＝－(x－)＋1で, y＝－x＋ (3) (2)で求めた直線とy軸の交点をCとする。△ABCの面積を求めよ。 【解】BC2＝()2＋(－1)2＝で,BC＝ △ABC＝××＝
２	須磨学園高校　（Ｒ７年）　★★★	５	立命館高校　（Ｒ７年）　★★★
(1) Dの座標とr の値を求めなさい。 【解】C2にy＝－1を代入して,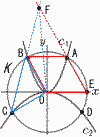－x2＝－1より, D(,－1) r＝OD＝√(()2＋(－1)2)＝2 (2) 点Aの座標とaの値を求めなさい。 【解】∠AOE＝60°OA＝r＝2より, A(1,) C1にA(1,)を代入して, 12a＝より, a＝ (3) 四角形OEABの面積を求めなさい。 【解】BA＝OE＝2,高さ＝ OEAB＝2×＝2 (4) 線分BCの長さと△OBCの面積を求めなさい。 【解】BC＝AD＝√{(－1)2＋(＋1)2}＝2 △OBC＝△OAD＝台形－三角形2つ 　＝(1＋)(＋1)－(××1)×2＝(2＋)－＝2 (5) △OFCの面積を求めなさい。 【解】△OFB＝△OAB＝×22＝…ア (4)より,△OBC＝2…イ　　△OFC＝ア＋イ＝2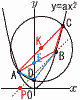＋		(1) aの値を求めなさい。 【解】y＝ax2にA(－4,4)を代入して,(－4)2a＝4より, a＝ (2) 円の面積を求めなさい。 【解】C(8,16) 中心K(2,10)より,半径KC＝6 円Kの面積＝(6)2π＝72πcm2 (3) △ABCと△APCの面積が等しくなる点Pの座標を求めなさい。ただし,点Pはx軸上にあり,点Pのx座標は点Ａのx座標よりも大きいものとします。 【解】Bを通るACの平行線は,y＝x＋3で,x軸との交点 P(－3,0) (4) △ADBの面積を求めなさい。 【解】KD＝KC＝6より, D(0,10－2√17) ABはy＝x＋6で, E(0,6) △ADE＋△BDE＝×(6－10＋2√17)(6＋4)＝10√17－20cm2
３	青山学院高等部　（Ｒ６年）　★★	６	明治大付属中野高校　（Ｒ６年）　★★
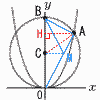(1) 点Aのx座標とkの値をaを用いて表せ。 【解】△ACHで,AC＝2a,CH＝aより, 　Aのx座標は√3a A(√3a,3a)を代入して, 　3a＝k(√3a)2より, k＝1/a (2) 点Mの座標をaを用いて表せ。 【解】OM:AM＝BO:BA＝2:1で,OM＝OA A(√3a,3a)より, M(√3a,2a) (3) △OCM:△OBAを求めよ。 【解】△OCM≡△BCM≡BAMより, △OCM:△OBA＝△OCM:3△OCM＝1:3		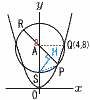点Ａ(0,8)を中心とする円が放物線y＝x2と異なる4点で交わっています。 (1) 点Pの座標を求めなさい。 【解】Q(q,8),P(p,p2)とすると,8＝q2より,Q(4,8) 半径ＡＱ＝AP＝4で,AP2＝(p－0)2＋(p2－8)2＝42 p4－28p2－192＝0より, P(2√3,6) (2) 点Sから直線PRに引いた垂線との交点をHとするとき,SHの長さを求めなさい。 【解】P(2√3,6),S(0,4)より,SP＝4で,△ASPは正三角形 高さSH＝AP＝×4＝2√3

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難