 関数 |
１１ 変域２ （略解） | |
| 関数 |
１１ 変域２ （略解） | |
| １ | 日本大第三高校 （Ｒ５年） ★★ | ５ | 慶應義塾高校 （Ｒ５年） ★ | ||||
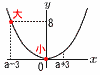 関数y＝ x2について,xの変域がa－3≦x≦a＋3のとき,yの変域はb≦y≦8である。定数a,bの値をそれぞれ求めなさい。ただし,－3＜a＜0とする。【解】(右図参照）上に開く放物線 －3＜a＜0より,xの変域は0を含むから, 最小値 x＝0のとき, b＝ ×02より, b＝0|a＋3|＜|a－3|だから,最大値はx＝a－3のとき, 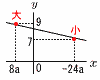(a－3)2＝8で, a＝－1 |
 a,bを定数とする。1次関数y＝ax＋bついて,xの変域が8a≦x≦－24aのとき,yの変域が7≦y≦9であったという。このとき,a＝( ), b＝（ ）である。【解】(右図参照） 8a≦－24aより,a＜0で,右下がりの直線 y＝ax＋bに,(8a,9)と(－24a,7)を代入して, 8a2＋b＝9…ア －24a2＋b＝7…イ アイを連立させて解くと, a＝－  b＝17/2 |
||||||
| ２ | 初芝橋本高校 （Ｒ7年） ★★ | ６ | 龍谷大付属平安高校 （Ｒ7年） ★★ | ||||
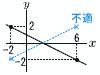 1次関数y＝ax＋bで,xの変域が－2≦x≦6のとき,yの変域が－2≦y≦2であるという。この１次関数のグラフがy軸の正の部分と交わるとき,a,bの値をそれぞれ求めなさい。【解】 ・2点(－2,－2)と(6,2)を通るとき,切片が負で不適 ・2点(－2,2)と(6,－2)を通るとき,切片は正で適
|
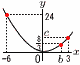 関数y＝ax2において，xの変域が－4≦x≦3のとき,yの変域はb≦y≦8です。このとき,a＝[ ], b＝[ ]となります。【解】 b≦y≦8より,上に開く放物線 －4≦x≦3より,最小値 b＝0 最大値はx＝－4のときで,y＝8 これを代入して,8＝(－4)2aより, a＝  |
||||||
| ３ | 函館ラ・サール高校 （Ｒ7年） ★★ | ７ | 立教新座高校 （Ｒ7年） ★★ | ||||
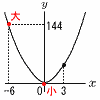 y＝(a＋1)x2でxの変域が －6≦x≦3のとき,yの変域はb≦y≦144であるという。a,bの値をそれぞれ求めなさい。【解】b≦y≦144より,上に開く放物線 －6≦x≦3より,最小値 b＝0 最大値はx＝－6のときで,y＝144 これを代入して,144＝(a＋1)×(－6)2 144＝36(a＋1)より, a＝3 |
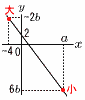 a,bを定数とします。1次関数y＝－4x＋2において,xの変域が－4≦x≦aのとき,yの変域は6b≦y≦－2bです。このとき,a,bの値を求めなさい。【解】傾きが負だから,右下がりの直線 2点(－4,－2b)と(a,6b)を通る
|
||||||
| ４ | 国学院大久我山高校 （Ｒ６年） ★★ | ８ | 大阪府立高校Ｃ （Ｒ６年） ★★ | ||||
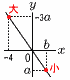 1次関数y＝－3x＋bにおいて,xの変域が－4≦x≦bのとき,yの変域はa≦y≦－3aである。このとき, a＝（ ）,b＝（ ）である。【解】(右図参照）右下がりの直線 最小値はx＝bのとき,y＝－3b＋b＝a…ア 最大値はx＝－4のとき,y＝－3×(－4)＋b＝－3a…イ アイを連立させて解くと, a＝－24/5, b＝12/5 |
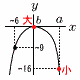 a,bを定数とする。関数y＝－ x2について,xの変域が－6≦x≦aのときのyの変域が－16≦y≦bであるとき,a,bの値をそれぞれ求めなさい。【解】(右図参照）下に開く放物線 最小値はx＝aのとき,y＝－ a2＝－16で, a＝8最大値は原点で, b＝0 |
||||||
