 関数 |
１０ 変域１ （略解） | |
| 関数 |
１０ 変域１ （略解） | |
| １ | 岡山白陵高校 （Ｒ７年） ★★ | ５ | 近畿大付属高校 （Ｒ５年） ★ | |||
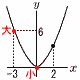 関数y＝ax2について,xの変域が−3≦x≦2のとき,yの変域は0≦y≦6である。aの値を求めよ。【解】(右図参照) 最小値が0だから,上に開く放物線 最大値 x＝−3のとき,y＝(−3)2a＝6 9a＝6より, a＝\(\color{red}{\frac23}\) |
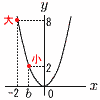 a,bは定数とする。関数y＝ax2について,xの変域が−2≦x≦bのとき,yの変域は2≦y≦8である。このとき,a,bの値を求めよ。 【解】(右図参照)下に凸の放物線 最大値 x＝−2のとき,(−2)2a＝8で, a＝2 最小値 x＝bのとき,2b2＝2で, b＝−1 |
|||||
| ２ | 東京科学大附属科技高校 （Ｒ７年） ★ | ６ | 大阪府立高校 （Ｒ７年） ★★★ | |||
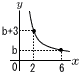 aを正の定数とする。関数y＝\(\frac{a}{x}\)について,xの変域が2≦x≦6のとき,yの変域はb≦y≦b＋3である。このとき,定数a,bの値をそれぞれ求めなさい。【解】(右図参照) ｙ＝\(\frac{a}{x}\)に2点の座標を代入して
|
a,bを定数とし,a＜b,c＝a＋3,d＝b＋3…ア とする。関数y＝ x2について,次の二つの条件を 同時に満たすa,bの値をそれぞれ求めなさい。 ・xの変域がa≦x≦bのときのyの変域は0≦y≦18である…イ ・xの変域がc≦x≦dのときのyの変域は0≦y≦8である…ウ 【解】(右図参照) 条件アよりa＜c＜0＜b＜d イより(a,18)のとき,a＝−6,c＝−3…エ イより(b,18)のとき,b＝6で,d＝9となって不適 ウより(c,8)のとき,c＝−4で,a＝−7となって不適 ウより(d,8)のとき,d＝4,b＝1…オ エオより, a＝−６, b＝１ |
|||||
| ３ | 桐光学園高校 （Ｒ６年） ★★ | ７ | 中央大附属横浜高校 （Ｒ７年） ★★ | |||
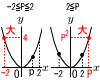 関数y＝x2について,xの変域が−2≦x≦pのとき,yの変域はq≦y≦p＋12である。このとき,定数p,qの値を求めよ。【解】(右図参照) ・−2≦p≦2のとき,(−2)2＝4＝p＋12 p＝-8となって,不適 ・p≧2のとき,p2＝p＋12で, p＝4 また, q＝0 |
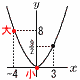 関数y＝x2について,xの変域がa≦x≦3のとき,yの変域がb≦y≦8である。 このとき,a,bの値を求めなさい。【解】(右図参照) 最大値は,x＝aのときで,y＝8だから, 8＝ a2より,a＝±4a≦3だから,a＝−4 最小値 b＝0 |
|||||
| ４ | ラ・サール高校 （Ｒ６年） ★★ | ８ | 明治大付属中野高校 （Ｒ６年） ★★★ | |||
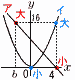 2つの関数y＝−3x＋a…アとy＝x2…イがあり,xの変域がb≦x≦4のとき,yの変域が一致するという。a,bの値の組をすべて求めよ。ただし,b＜0とする。【解】(右図参照) イの最小値は0で,アの最小値と一致するから −3×4＋a＝0で, a＝12 アの最大値はx＝bのときで,−3b＋12＝16より, b＝−  |
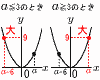 関数y＝ x2について,xの変域がa−6≦x≦aのとき,yの変域が0≦y≦9となります。このとき,aの値をすべて求めなさい。【解】(右図参照) ・a≦3のとき, (a−6)2＝9より, a＝6-3√3・a≧3のとき, a2＝9より, a＝3√3 |
|||||
