 関数 |
７ グラフの利用１ （略解） | |
| １ | 京都成章高校 （Ｒ7年） ★★★ | ２ | 盈進高校 （Ｒ５年） ★★ | ||||
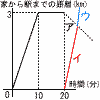 グラフは「Ａ君が家を出てからの時間とＡ君がいる場所の関係」を表したものである。家に戻るときの歩く速さを分速100mとしたとき,(1) A君が自転画で移動する画さは分違例ｍであるか求めなさい。 【解】3000÷10＝分速300m (2) Ａ君が自転単を修理していた時間は何分間か求めなさい。 【解】20−10＝10分 (3) Ａ君が家を出て20分後にＡ君の母親が車で家から駅に一定の速さで向かった。車の速さが時速42kmのとき,2人は何時何分何秒に出会うか求めなさい。 【解】
 で, 7時23分45秒(4) (3)のとき,Ａ君は母親の車に乗車し，駅に向かうことにした。すると,本来自転車を利用して駅に到着する時刻より5分早く着くことができた。このとき．Ａ君が乗車してからの車の速さは時速何kmであるか求めなさい。ただし,Ａ君と母親が出会ってから乗車するまでの時間は考えないものとする。またＡ君が乗車してからの車の速さは一定であるとする。 【解】ウは本来(40,12)を通るから,速さをaとすると, a(35−95/4)＋21/8＝12より, a＝  km/分＝50km/時 |
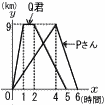 次のグラフは,9km離れた2地点A,B間をPさんとQ君がA地点を同時に出発して往復した様子を示したものである。xはPさんとQ君がA地点を出発してからの時間を,yはA地点からの道のりを表している。(1) PさんがA地点を出発してB地点に着くまでのxとyの関係式を求めなさい。 【解】原点を通る直線 y＝axに(4,9)を代入して, 9＝4aで,a＝  式は, y＝  x …ア(2) Q君が,B地点からA地点にもどるときの速さは毎時何kmですか。また,この間のxとyの関係式を求めなさい。 【解】(2,9)と(5,0)を通る直線 9kmを3時間だから,9÷3＝3kmで,毎時3km y＝−3x＋bに(5,0)を代入して, 0＝−15＋b b＝15で, 式は y＝−3x＋15 …イ (3) Q君は,B地点からA地点にもどる途中,Pさんと出会いました。その地点は,B地点から道のりが何kmの地点かを答えなさい。 【解】出会い地点はアとイの交点 ア＝イより, x＝−3x＋15で,x＝ これをアに代入して,y＝ ×＝45/7Bからの道のり＝9−(45/7)＝18/7km |
||||||
| ３ | 熊本県立高校 （Ｒ５年） ★ | ４ | 慶應義塾高校 （Ｒ６年） ★★★ | ||||
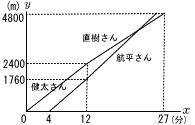 健太さんと直樹さんは,航平さんと,運動公園にある１周2400mのジョギングコ−スを走った。3人ともスタート地点から同じ方向に一定の速さで走り,健太さんと直樹さんは,健太さんから直樹さんの順にそれぞれ１周ずつ,航平さんは一人で2周走った。(1) 航平さんの走る速さは毎分何ｍか,求めなさい。 【解】1760mを8分 1760÷(12−4)＝200 毎分220ｍ (2) 航平さんが直樹さんと並んだのは,健太さんが走り始めてから何分何秒後か,求めなさい。 【解】2直線の交点 ・直樹の式は,2点(12,2400)と(27,4800)を通る から, y＝160x＋480 …ア ・航平の式は,傾き220で,(4,0)を通るから, y＝220x−880 …イ ア＝イより,x＝  で, 22分40秒後 |
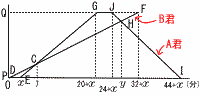 A君はP地点を出発してから20分後にQ地点に到着し,そこで4分間休憩した後に再び20分かけてP地点に戻ってきた。B君はA君より数分早くP地点を出発し,出発してから7分後にA君に追い抜かれ,A君がQ地点を出発してから8分後にQ地点に到着した。(1) A君がP地点を出発したのは,B君が出発してから何分後か。 【解】(右図参照) B君出発のx分後にA君が出発したとすると, グラフで,△CDE∽△CFGより,CD:CF＝DE:FG 7:{(32＋x)−7}＝x:(4＋8) これを解いて, x＝3分後 (2) A君がQ地点を出発した後にB君とすれ違うのは,B君がP地点を出発してから何分後か。 【解】 B君出発のy分後にすれ違ったとすると, グラフで,△HDI∽△HFJより,HD:HF＝DI:FJ y:{(32＋3)−y}＝(44＋3):8 これを解いて, y＝329/11分後 |
||||||
x