 関数 |
６ 一次関数４ （略解） | |
| １ | 宇都宮短大附属高校 （Ｒ７年） ★ | ５ | 駿台甲府高校 （Ｒ５年） ★★★ | ||||||||
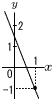 １次関数y＝ax＋bのグラフが右の図のようになっているとき,不等式 m＜a＜m＋1 を満たす整数mの値は[ ]である。【解】傾きaは負の整数, 1＜切片b＜2 ・b＝1のとき,傾きa＝−2 ・b＝2のとき,傾きa＝−3 −3＜a＜−2であればよいから, m＝−3 |
右図で,直線l の式はy＝ x…ア,直線mの式はy＝− x…イである。直線l 上にx座標が正である点Pがあり,点Pを通り,傾きが− である直線をn,2直線m,nの交点をQとする。(1) 点Pのx座標が2であるとき,点Qの座標 【解】アにx＝2を代入して,P(2,1) nは,y＝− (x−2)＋1で,y＝−x＋6…ウQはmとnの交点で,− x＝−x＋6より,x＝ イにx＝2を代入して, Q(,  − )(2) 2点P,Qのy座標の差が１であるとき,点Qの座標 【解】Q(4t,−t)とすると, nは,y＝− (x−4t)−tで,y＝−x＋9t…エPはl とnの交点で, 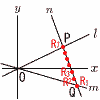x＝−x＋9tより,P(3t, t) y座標の差＝t−(−t)＝1で,t＝  よって, Q( ,− )(3) 2点P,Qがともに格子点で,線分PQ上にある格子点の個数が７個のとき,点Qの座標 【解】nの傾きは− だから,7個の格子点をR1,R2,…,R7とすると, Q＝R1(4t,−t),R2(4t−2,−t＋5), ……R7(4t−12,−t＋30)＝P R7をアに代入して,−t＋30＝ (4t−12)で,t＝12よって,Q(4t,−t)＝Q(48,−12) |
||||||||||
| ２ | 帝塚山泉ヶ丘高校 （Ｒ７年） ★★★ | ||||||||||
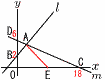 図において,2つの直線l：y＝x＋2と m：y＝− x＋6の交点をA,l とy軸との交点をB,mとx軸との交点をCとする。(1) Aの座標を求めなさい。
【解】B(0,2) C(18,0) △DOC−△DBA＝ ×6×18−×4×3＝54−6＝48(3) Aを通り四角形ABOCを２等分する直線とx軸との交点の座標を求めなさい。 【解】 △AEC＝ ×EC×5＝48×より,EC＝48/5OE＝18−48/5＝42/5で, (42/5,0) |
|||||||||||
| ３ | 立教新座高校 （Ｒ５年） ★★ | ６ | 芝浦工大附属高校 （Ｒ５年） ★ | ||||||||
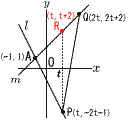 。P,Qのx座標がともにAのx座標よりも大きく,△APQの面積が54となるようなtの値を求めなさい。【解】 A(−1,1) P(,−2t−1) Q(2t,2t＋2) R(t,t＋2) △APQ＝ ×(PとRのy座標差)×(AとQの座標差)＝ {(t＋2)−(−2t−1)}{2t−(−1)}＝ (3t＋3)(2t＋1)＝(t＋1)(2t＋1)＝54(2t−7)(t＋5)＝0となって,t＞0より, t＝  |
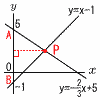 2直線y＝− x＋5とy＝x−1とy軸によって囲まれた部分の面積を求めなさい。【解】 交点Pのx座標を求める − x＋5＝x−1より,x＝18/5△PAB＝ ×6×(18/5)＝54/5 |
||||||||||
| ４ | 青森県立高校 （Ｒ６年） ★★★ | ７ | 久留米大附設高校 （Ｒ６年） ★★★ | ||||||||
方程式 2x＋y＝3 について述べた文として適切でないものを,次のア〜エの中から1つ選び,その記号を書きなさい。
【解】傾きは−2だから, エ |
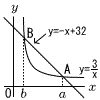 座標平面上において,直線y＝−x＋32と反比例y＝ のグラフの交点をA,Bとし,A,Bのx座標をそれぞれa,bとする。ただし,a＞b＞0とする。(1) aの値を求めよ。 【解】−x＋32＝ より,x2−32x＋3＝0これを解いて,a＝16＋√253 (2) ＡとＢの距離をdとするとき,d2の値を求めよ。 【解】直線ABの傾きは−1だから,AB＝√2(a−b) d2＝2(a−b)2＝2(2√253)2＝2024 |
||||||||||
