| １ | 福島県立高校 （Ｒ７年） ★ | ６ | 大阪産大附属高校 （Ｒ７年） ★★ | |||||||||||
| yがxの1次関数で,変化の割合が2で,x＝－3のときy＝7となる1次関数の式を求めなさい。 【解】 変化の割合＝傾き＝2 y＝2(x＋3)＋7より, y＝2x＋13 |
点Aは2点(3,－4),(2,－1)を通る直線上の点で,x座標が－2である。このとき,点Ａのy座標を求めなさい。
これにx＝－2を代入すると, y=－3×(－2)＋5＝11 |
|||||||||||||
| ２ | 市立福山高校 （Ｒ５年） ★★ | ７ | 関西大倉高校 （Ｒ７年） ★★★ | |||||||||||
| ３つの直線y＝x－7,y＝－2x＋8,y＝axがあります。a＝2のとき,この3つの直線は交わり三角形ができます。この3つの直線で三角形ができないようなaの値は全部で何個あるか,その個数を求めなさい。 【解】 ・a＝1のとき,ア∥ウ ・a＝－2のとき,イ∥ウ ・a＝－のとき,ウはアイの交点(5,－2)を通る よって,三角形ができないaは 3個 |
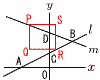 右の図のように2点Ａ(－4,0),B(4,4)を通る直線l と,点Bを通り傾きが－ である直線mがある。直線l,mとy軸の交点をそれぞれC,Dとする。(1) 直線l の式を求めよ。
 (x＋4)＋0より, y＝x＋2（2）△OBDと△BCPの面積が等しくなるように直線m上に点Pをとる。点Pの座標を求めよ。ただし,点Pのx座標は負とする。 【解】mはy＝－ (x－4)＋4＝－x＋\(\frac{16}{3}\)D(0,\(\frac{16}{3}\))で,△OBD＝ ×\(\frac{16}{3}\)×4＝\(\frac{32}{3}\)…ア点Pのx座標をkとすると,△OBD＝△BCP＝△PDC＋△BDC ＝ ×(\(\frac{16}{3}\)－2)×(4－k)＝ (4－k)＝\(\frac{32}{3}\)となればよい4－k＝\(\frac{32}{3}\)×  より,k＝4－\(\frac{32}{5}\)＝－\(\frac{12}{5}\)で,P(－\(\color{red}{\frac{12}{5}}\),\(\color{red}{\frac{92}{15}}\))(3) (2)のとき,線分BC上に点Rをとり,正方形PQRSを作る。ただし,辺PQはy軸と平行である。このとき,点Rの座標を求めよ。途中の考え方や式も記入すること 【解】R(t, t＋ 2)とすると,PQ＝QRだから,\(\frac{92}{15}\)－( t＋2)＝t－\(\frac{12}{5}\)より,t＝\(\frac{52}{45}\)よって, R(\(\color{red}{\frac{52}{45}}\),\(\color{red}{\frac{116}{45}}\)) |
|||||||||||||
| ３ | 土浦日大高校 （Ｒ６年） ★★ | |||||||||||||
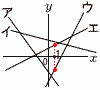 1次関数y＝ax＋bについて,(1) a＞0,b＜0のとき 【解】傾きaが正,切片bが負で, ウ (2) a＋b＞0,ab＜0のとき, 【解】イかウだが,x＝1のとき,y＝a＋b＞0で, x軸より上となるから, イ ４ |
||||||||||||||
| ５ | 広島県立高校 （Ｒ５年） ★★ | ７ | 國學院大久我山高校 （Ｒ５年） ★ | |||||||||||
y軸上に点A (0,8))があり,関数y＝ x＋2…ア のグラフ上にx＞0の範囲で動く2点B,Cがあります。(1) ACがx軸に平行となるとき,線分ACの長さ 【解】アにy＝8を代入して 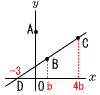 8＝x＋2より,x＝9で, AC＝9(2) DB＝BCのとき,直線ACの傾き 【解】アにy＝0を代入して,D(－3,0) Bのx座標をbとすると, DBの(x座標差)＝BCの(x座標差)より, b－(－3)＝4b－bで,b＝ 
|
(1) 異なる2点(p,p2),(q,q2)を通る直線の傾き 【解】
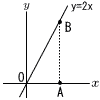 (2) 図のように,直線y＝2x, 2点A(1,0),B(1,b)がある。 ① bの値を求めなさい。 【解】 y＝2xに(1,b)を代入して, b＝2×1＝2 ② ＯＢの長さを求めなさい。 【解】 B(1,2)より, OB＝√12＋22＝√5 |
|||||||||||||
