| 4 一次関数2 (略解) | ||
| 4 一次関数2 (略解) | ||
| 1 | 愛知県立高校 (R7年) ★ | 5 | 秋田県立高校 (R7年) ★ | ||||||||
| 2直線y=x-3, y=-2x-6 の交点を通り,直線y=2x+1に平行な直線の切片として正しいものを,次のアからエまでの中から一つ選びなさい。 ア -4 イ -2 ウ 0 エ 4
|
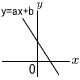 右の図のような1次関数y=ax+b(a,bは定数)のグラフがある。このときのa,bについて,式の値が必ず正の数となるものを,次のア~エから1つ選んで記号を書きなさい。 右の図のような1次関数y=ax+b(a,bは定数)のグラフがある。このときのa,bについて,式の値が必ず正の数となるものを,次のア~エから1つ選んで記号を書きなさい。ア a+b イ a-b ウ b-a エ ab 【解】右下がりの直線 傾きa<0, y切片b>0より, b-a>0で ウ |
||||||||||
| 2 | 龍谷大付属平安高校 (R7年) ★ | 6 | 帝京高校 (R7年) ★ | ||||||||
| 直線l は2点(-2,5),(a,-3)を通り,直線,y=- 【解】(-2,5)を通り,傾き- y=- これに(a,-3)を代入して,-3=- |
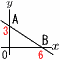 原点をOとし,y軸と点A(0,3),x軸と点Bで交わる直線ABがある。三角形AOBの面積が9となるとき,直線ABの式は[ ]です。ただし,直線ABの傾きは負であるものとする。 原点をOとし,y軸と点A(0,3),x軸と点Bで交わる直線ABがある。三角形AOBの面積が9となるとき,直線ABの式は[ ]です。ただし,直線ABの傾きは負であるものとする。【解】高さ3だから,底辺が6になればよい B(6,0)で, y=- |
||||||||||
| 3 | 東京学芸大附属高校 (R6年) ★ | 7 | 芝浦工大附属高校 (R7年) ★★ | ||||||||
| アメリカなどの国では日本とは異なる単位が使われることがある。時速40kmで進む自動車Aがx時間進んだときの道のりをykmとして,yをxの式で表すとy=40xである。 自動車Aと同じ速さで進む自動車Bがx時間進んだときの道のりをzマイルとして,zをxの式で表しなさい。ただし,1マイルは1.6kmであるとする。 【解】zマイル=1.6zkm=40x
|
【解】
y軸対称だから ,y=- |
||||||||||
| 4 | 千葉県立高校 (R5年) ★★ | 8 | 東北高校 (R5年) ★★ | ||||||||
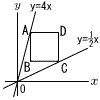 正方形ABCDがある。 正方形ABCDがある。(1) 点Aのy座標が8であるとき. ① 点Aのx座標を求めなさい。 【解】アにy=8を代入して 8=4xで, x=2 ② 2点A,Cを通る直線の式を求めなさい。 【解】ACはA(2,8)を通って,傾き-1 y=-(x-2)+8で, y=-x+10 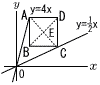 (2) 点Dの座標を求めなさい。 【解】□ABCDの1辺を2aとすると, Aのx座標=13-aで,これをアに代入して, Aのy座標=4(13-a)…ウ Cのx座標=13+aで,これをイに代入して, Cのy座標= ウ-エ=2aより,4(13-a)- これを解いて,a=7 A(6,24) C(20,10)となるから, D(20,24) |
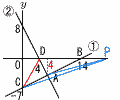 直線①は関数y= 直線①は関数y=(1) aの値を求めなきい。 【解】②は,x切片4,y切片8 ②の傾きa=-8÷4=-2 (2) 点Aの座標を求めなさい。 【解】①y= (3) △ACDの面積を求めなさい。 【解】△ACD=△BCD-△BAD △ACD= (4) x軸上に,x座標が点Bのx座標より大きい点Pをとります。△ACPの面積が△ACDの面積の 【解】P(t,0)とする △ACP= |
||||||||||