 
|
 平方数 平方数
112=121 122=144 132=169 142=196
152=225 162=256 172=289 182=324
192=361 252=625 |
 2の累乗 2の累乗
22=4 23=8 24=16 25=32 26=64
27=128 28=256 29=512 210=1024
(2進法でよく使うよ) |
 0の割り算 (0では割れない) 0の割り算 (0では割れない)
0÷1=0
1÷0=解なし (不能)
0÷0=すべての実数 (不定)
|
 倍数の見分け方 倍数の見分け方
3の倍数=(各位の数の和) が3の倍数
9の倍数=(各位の数の和) が9の倍数
4の倍数=(下二桁) が4の倍数
8の倍数=(下三桁) が8の倍数 |
 3で割ったときの数 3で割ったときの数
3で割り切れる数(3の倍数)=3k (kは整数)
3で割ったとき 1 余る数=3k+1 (kは整数)
3で割ったとき 2 余る数=3k+2 (kは整数)
|
 Nのすべての約数 Nのすべての約数
N=ax×by×cz の約数
| ・ 表し方 … |
(a1〜x) |
× |
(b1〜y) |
× |
(c1〜z) |
| ・ 個 数 … |
x+1個 |
|
y+1個 |
|
z+1個 |
・360(23×32×51)は, 4×3×2=24個の約数がある |
 0と1の約数・倍数 0と1の約数・倍数
・1は,すべての整数の約数
⇒約数に1を入れ忘れるな!
(逆に,すべての整数は1の倍数)
・0は,すべての整数の倍数
⇒倍数に0を入れ忘れるな!
(しかし,どの整数も0の約数ではない) |
 公約数と公倍数 公約数と公倍数
・すべての公約数は,最大公約数の約数
12と18の最大公約数=6
12と18の 全 公約数=1,2,3,6
・すべての公倍数は,最小公倍数の倍数
4と6の最小公倍数=12
4と6の 全 公倍数=12,24,36,48,… |
 連続整数の積 連続整数の積
・連続2整数の積は,2で割り切れる。
(2整数の中に,2の倍数が1つ含まれるから)
5×6 48×49
・連続3整数の積は,3で割り切れる。
(3整数の中に,3の倍数が1つ含まれるから)
5×6×7 48×49×50 |
 比の値 比の値
たとえば
| x |
= |
y |
のとき, |
x |
= |
y |
=k とおき, |
| 2 |
3 |
2 |
3 |
x=2k,y=3k としてみる。
|
 連比 連比
たとえば
| x:y:z=1:2:3 のとき,( |
x |
= |
y |
= |
z |
も同様) |
| 1 |
2 |
3 |
x=k,y=2k,z=3k としてみる。 |
 指数法則 指数法則
xa×xb=xa+b xa÷xb=xa-b
(xy)a=xaya (xa)b=xab
x0=1 x−2=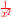 |
 乗法公式 乗法公式
(x+a)(x+b)=x2+(a+b)x+ab
(ax+b)(cx+d)=acx2+(ad+bc)x+bd
(x+y+z)2=(x2+y2+z2)+2(xy+yz+zx)
|
 基本対称式 x+y と xy 基本対称式 x+y と xy
・x2+y2=(x+y)2−2xy
・(x−y)2=(x+y)2−4xy
・x3+y3=(x+y)3−3xy(x+y)
・x2+y2+z2=(x+y+z)2−2(xy+yz+zx) |
 分母が文字の方程式 分母が文字の方程式
| 1 |
+ |
2 |
=5では, X+2Y=5 と置き換え |
| x |
y |
| このとき, |
1 |
=X, |
1 |
=Y としている。 |
| x |
y |
|
 ルートの概数語呂合わせ ルートの概数語呂合わせ
√2=1.414 √3=1.732 √5=2.236
(一夜一夜に人見頃) (人並みにおごれや) (富士山麓オウム鳴く)
√6=2.450 √7=2.645 √10=3.162
(煮よ,良く良く) (菜に虫いない) (三色に並ぶ) |
 分母の有理化 分母の有理化
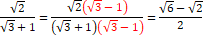

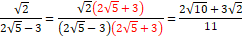 |
 無理数の小数部分 無理数の小数部分
・√5では,2<√5<3だから
(整数部分)=2,(小数部分)=√5−2
・√23では,4<√23<5だから
(整数部分)=4,(小数部分)=√23−4 |
 x=p,qが解となる2次方程式 x=p,qが解となる2次方程式
a(x−p)(x−q)=0 (ただし,a≠0)
したがって,ax2−a(p+q)x+apq=0
・x=−2,3が解となる2次方程式は
a(x+2)(x−3)=0 つまり,ax2−ax−6a=0 |
 解と係数の関係 (高校内容) 解と係数の関係 (高校内容)
ax2+bx+c=0の解がx=p,qのとき
| 解の和 p+q=− |
b |
,解の積 pq= |
c |
| a |
a |
・x2−3x+1=0では,
解の和 p+q=3,解の積 pq=1 |