データの活用	２８　余事象 (確率)　（略解）
以下の問題では,どの事柄が起こることも同様に確からしいものとします。

１	専修大附属高校　（Ｒ５年）　★★	５	大手門学院大手前高校　（Ｒ６年）　★
A,B,C,D,E の5人から2人を選ぶとき,Aが選ばれない確率を求めなさい。 【解】 (Aが選ばれない)確率＝(A以外の2人を選ぶ)確率 　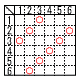確率＝ 4C2 ＝ 4×3÷2 ＝ 3 5C2 5×4÷2 5		2個のさいころを同時に投げるとき,出る目の和が4の倍数にならない確率を求めなさい。 【解】 和が4の倍数は右表(〇)より,9通り 　確率＝1−(9/36)＝
２	立女子第二高校　（Ｒ７年）　★★	６	京都府立山城高校　（Ｒ７年）　★★★
さいころを3回振り,2回以上同じ目が出る確率を求めなさい。 【解】1−(すべて異なる目)の確率 すべて異なる目の出方は,6×5×4＝120通り 　確率＝1− 120 ＝1− 120 ＝1− 5 ＝ 4 63 216 9 9		1から4までの数が1つずつ書かれた4枚のカードがある。この4枚のカードを箱に入れて;そこから１枚を取り出す。そのカードに書かれた数を確認してから,カードを箱に戻す。この操作を3回行ったとき,確認した3つの数の積が4以上の偶数となる確率を求めよ。 【解】1−(積が3以下,または奇数)の確率 (1,1,1) (3,3,3,) が各1通り　(1,1,2) (1,1,3) (1,3,3) が各3通り 　確率＝1−(1×2＋3×3)÷43＝1−11/64＝53/64
３	桐光学園高校　（Ｒ４年）　★★★	７	慶応義塾志木高校　（７年）　★★★
大中小の3個のさいころを同時に投げ,出た目の数の積を考える。 (1) 積が奇数となる確率を求めよ。 【解】3数すべて奇数のとき, 　確率＝()3＝ (2) 積が5の倍数となる確率を求めよ。 【解】少なくとも1数が5 　確率＝1−(3数すべて5以外)3 　　　　＝1−()3＝91/216 (3) 積が8の倍数となる確率を求めよ。 【解】8の倍数にならない場合を考える ・奇数3個…()3＝ ・奇数2個と偶数1個…()2××3＝ ・奇数1個と(2か6)2個…×()2×3＝ 　確率＝1−(8の倍数にならない)確率 　　＝1−(＋＋)＝1−＝		袋の中にKと書いてある玉が1個,Eと書いてある玉が2個,Ｉ と書いてある玉が3個,Oと書いてある玉が4個人っている。この中から3個の玉を取り出すとき,2種類の玉が出る確率を求めよ。 【解】1−(1種類か3種類)の確率 3個の取り出し方は全部で,(10×9×8)÷(3×2)＝120通り 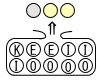1種類 　・( I, I, I) 型は1通り 　・(O,O,O)型は4C3＝4通り 3種類 　・(K,E,I)型は2×3＝6通り 　・(K,E,O)型は２×4＝8通り 　・(K,I,O)型は3×4＝12通り 　・(E,I,O)型は2×3×4＝24通り 　確率＝1− 1＋4＋6＋8＋12＋24 ＝1− 55 ＝ 13 120 120 24
４	東京工大附属科技高校　（Ｒ６年）　★	８	富山県立高校　（Ｒ６年）　★
4本のうち2本のあたりくじが入っているくじがある。A,Bの2人がこの順に1本ずつくじをひき,ひいたくじはもどさないとき,少なくとも1人はあたりくじをひく確率を求めなさい。 【解】 (少なくとも1人はあたり)の確率＝1−(2人ともはずれ)の確率 　確率＝1−×＝1−＝		袋の中に1,2,3,4,5の数が1つずつ書かれた同じ大きさの玉が5個人入っている。中を見ないで,この袋から同時|こ2個の玉を取り出すとき,取り出した玉に書かれた数の積が偶数となる確率を求めなさい。 【解】(積が偶数)の確率＝1−(積が奇数)の確率 積が奇数は,(1,3) (1,5) (3,5) の3通り 取り出し方は全部で,5×4÷2＝10通り 　確率＝1−＝

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難