 データの活用 |
２７ その他 (確率) （略解） |
| 以下の問題では,どの事柄が起こることも同様に確からしいものとします。 | |
| データの活用 |
２７ その他 (確率) （略解） |
| 以下の問題では,どの事柄が起こることも同様に確からしいものとします。 | |
| １ | 沖縄県立高校 （Ｒ６年） ★★★ | ４ | 専修大附属高校 （Ｒ７年） ★★ | ||||||||||||
| A,B,C,Dの4人がプレゼントをーつずつ持ちより,交換会を開く。プレゼントはすべて異なるものとし,A,B,C,Dの4人が用意したプレゼントをそれぞれa,b,c,dとする。 (1) プレゼントの受け取り方は全部で何通りあるか答えなさい。 【解】4×3×2×1＝24通り (2) Aさんがaではないプレゼントを受け取る確率を求めなさい。  【解】Aさんは3通り確率＝(3×3×2×1)÷24＝18/24＝  (3) A,B,C,Dの4人全員が,自分で用意したプレゼントを受け取らない確率を求めなさい。 【解】自分のを受け取らないのは,右表より9通り 確率＝9÷24＝  |
A,B,C,D,Eの5人から3人を選ぶとき,Aが選ばれる確率を求めなさ い。 【解】B,C,D,Eの4人から2人を選ぶ
|
||||||||||||||
| ５ | 早稲田佐賀高校 （Ｒ６年） ★★ | ||||||||||||||
| AのボールがBのボールよりも右にくる確率 【解】並べ方は全部で,4×3×2×1＝24通り ・A〇〇〇のとき,0通り ・〇A〇〇のとき,1通り ・〇〇A〇のとき,4通り ・〇〇〇Aのとき,6通り 確率＝(0＋2＋4＋6)÷24＝  |
|||||||||||||||
| ２ | 愛光高校 （Ｒ５年） ★★★ | ６ | 立教新座高校 （Ｒ５年） ★★★ | ||||||||||||
直線y＝ x＋cをl とするとき,(1) l が直線y＝2xと平行になる確率を求めよ。 【解】b＝2aのとき (a,b)＝(1,2) (2,4) (3,6) (4,8) (5,10) の5通り 確率＝5÷(6×10)＝  (2) l が点(6,10)を通る確率を求めよ。 【解】10＝ ×6＋cのとき,・c＝4のとき, (a,b)＝(1,1) (2,2) (3,3) (4,4) (5,5) ・c＝3のとき, (a,b)＝(6,7) ・c＝2のとき, (a,b)＝(3,4) (6,8) ・c＝1のとき, (a,b)＝(2,3) (4,6) (6,9) 全部で12通りだから,確率＝12÷(6×10×4)＝  |
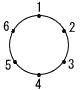 図のように,円周を6等分した点にそれぞれ1から6までの数字がついています。さいころを3回投げて,出た目と同じ数字の点を結んでできる図形を考えます。(1) 三角形にならない確率 【解】三角形にならない確率＝1－(なる確率) ＝1－(3回とも異なる目の確率)
【解】1つの直径に対して4個で,順を考慮すると, (4×3)×6＝72個で, 確率＝72÷63＝  |
||||||||||||||
| ３ | 西大和学園高校 （Ｒ７年） ★★★ | ７ | 早大高等学院 （Ｒ６年） ★★★ | ||||||||||||
| 正四面体の形をした箱があり,面がそれぞれ赤色,青色,黄色,緑色で塗られている。箱を4回,転がして,底になった面に順に1,2,3,4を記入していく。例え
ば,底の面の色が順に赤色,青色,赤色,黄色であった場合には,赤色の面に1,3,青色の面に2,黄色の面に4が記入され,緑色の面には何も記入されないことになる。このとき,次の確率を求めよ。 (1) 赤色の面に1,青色の面に2,黄色の面に3,緑色の面に4が記入される確率。 【解】色の出方は全部で,44＝256通りで, 確率＝1/256 (2) 数が記入されている面が1面だけである確率。 【解】4回とも同色で, 確率＝(1/4)4×4＝1/64 (3) すべての面に数が記入される確率。 【解】4回とも異色で,出方＝4×3×2×1＝24通り 確率＝24÷256＝3/32 (4) 赤色の面と黄色の面の,ちょうど2面に数が記入される確率。 【解】赤3回黄1回, 赤2回黄2回, 赤1回黄3回 赤と黄だけの出方は24＝16通り,そのうち全て赤か黄は2通り 確率＝(16－2)÷256＝14/256＝7/128 |
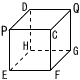 (1) Pから出発して,1秒後にAB＝√2となる確率【解】A,Bが移動可はC,D,Eの各3点で,9通り このうち,AB＝√2となるのは, CD,CE,DEで(逆も含めて)6通りで,確率＝＝  (2) P,Qから出発して,その1秒後もAB＝√2となる確率 【解】AはC,D,Eの3点,,BはC,D,Gの3点へ移動できる このうち,AB＝√2となるのは,CD,DC,CE,DE,CG,DG,EGの7通り 確率＝7÷32＝  (3) Pから出発して,2秒後にAB＝√3となる確率 【解】AB＝√3となるのは,PG,CH,QE,DFだが, いずれも2秒後には移動できないから,確率＝0 (4) Pから出発して,その3秒後にAB＝√2となる確率 【解】AB＝√2となるのは,A,Bが正方形の対角点 ・(1)より,同一点出発の場合の確率は 正方形の対角点に到着が  , 同一点到着が ・(2)より,正方形の対角点出発の場合の確率は 正方形の対角点に到着が  , 同一点到着が 左の表より,確率＝ ××＋××＋××＋××＝（98＋24＋42＋18）/35＝182/243 |
||||||||||||||