 データの活用 |
１２ 数列１ （略解） |
| データの活用 |
１２ 数列１ （略解） |
| １ | 宇都宮短大附属高校 （Ｒ４年） ★★ | ５ | 近畿大附属和歌山高校 （Ｒ５年） ★ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3で割ると2余る自然数で7番目の数と,5で割ると3余る自然数で10番目の数の和は[ ]である。 【解】 3m＋2にm＝6を代入して,3×6＋2＝20…ア 5n＋3にn＝9を代入して,5×9＋3＝48…イ ア＋イ＝20＋48＝68 |
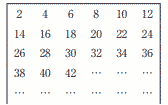 右の図のように,連続する偶数を2から順に6個ずつ並べる。(1) この図で上から6番目で左から4番目の数を求めよ。 【解】 8, 20, 32 ,44, 56, 68 (2) 上からm番目で左からn番目の数をm,nを用いて表せ。 【解】 右端の列は12の倍数で,m番目は12m 左からn番目＝右端より2(6−n)小さい よって, 12m−2(6−n)＝12m＋2n−12 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ２ | 明治学院東村山高校 （Ｒ５年） ★★ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
39番目の分数を答えな さい。 【解】群の項数を足していくと, 1＋2＋…＋7＋8＝36 39番目は,9群の3項目 よってｋ＝9より, 3/10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ３ | 尚絅学園高校 （Ｒ５年） ★ | ６ | 鎌倉学園高校 （Ｒ７年） ★★★ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
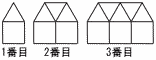 図のように,1辺が1cmの正三角形と正方形を規則的に並べて,(1) 5番目の正三角形の個数 【解】1,3,5,7,9,…で, 9個 (2) n番目の正三角形と正方形の個数の合計 【解】 ・正三角形…2n−1 ・正方形…n よって, 2n−1＋n＝(3n−1)個 (3) 周りの長さが25cmである図形には,正三角形と正方形が合わせて何個並んでいますか。 【解】・正三角形…n＋1 ・正方形…n＋2 (n＋1)＋(n＋2)＝25より, n＝11 (2)に代入して, 3×11−1＝32個 |
1からnまでの自然数の積をSnと表します。 例えば,Ｓ1＝1, Ｓ2＝1×2, Ｓ3＝1×2×3 となります。 (1) S1＋S2＋S3＋S4を求めなさい， 【解】 1＋2＋6＋24＝33 (2) S1＋S2＋…＋S6を6で割ったときの余りを水めなさい。 【解】S3〜S6は6で割り切れるから,S1＋S2＋6ｋ(ｋは自然数) S1＋…＋S6＝1＋2＋6k＝3＋6kで,余りは3 (3) S1＋S2＋…＋S100を420で割ったときの余りを求めなさい。 【解】420＝3×4×5×7だから,S7〜S100は420で割り切れる (S1＋…＋S6)÷420＝873÷420＝2余り33 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ４ | 東洋大京北高校 （Ｒ６年） ★ | ７ | 芝浦工大附属高校 （Ｒ６年） ★★ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
下の図のように,ある規則に従って自然数を並べます。
(1) 30は何段目の左から何番目にあるか答えなさい。 【解】x段目の末項はx2 52＜30＜62だから,6段目(26,27,…,30,…,36)の5番目 (2) x段目の一番右の数をxを使って表しなさい。 【解】x2 (3) x段目の左からy番目の数をx,yを使って表しなさい。 【解】x段目は(x−1)2＋1, (x−1)2＋2, … ,x2 よって, (x−1)2＋y |
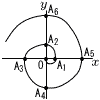 座標平面上に渦巻線がある。(1) 次の空欄をうめなさい。 （ｱ）点A2024の座標は[（0,−2024)]である。 （ｲ）3点A14,A15,A16を頂点とする三角形の面積は[ ] 【解】  ×(14＋16)×15＝225(2) 3点Ak,Ak+1,Ａk+2を頂点とする三角形の面積をSkとする (ｱ) Sk+1−Ｓk＝35となるkの値を求めよ。 【解】Sk＝ (k＋k＋2)(k＋1)＝(k＋1)2Sk+1−Ｓk＝(k＋1＋1)2−(k＋1)2＝2ｋ＋3＝35で, ｋ＝16 (ｲ) Sa−Sb＝48となる(a,b)の組を求めよ。 【解】Sa−Sb＝(a＋1)2−(b＋1)2＝(a−ｂ)(ａ＋ｂ＋2)＝48
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
