| 32 球 (略解) | ||
| 32 球 (略解) | ||
| 1 | 都立産業技術高専 (R5年) ★★ | 4 | 久留米大附設高校 (R6年) ★★ |
| 半径rcmの球が,点Pで平面Hと接している。 (1) r=3のとき,球Oの体積 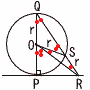 【解】球O= 【解】球O=(2) ∠SQOと∠ROPの比 【解】△SORと△OSQは二等辺三角形 ∠SQO=2aとすると,∠ROP=3aで, 2:3 (3) 線分QSの長さ 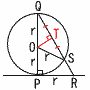 【解】OからQRに垂線OTをおろす 【解】OからQRに垂線OTをおろす△PQRで,QR=√(2r)2+r2= △QTO∽△QPR(比1: QT=2r×(1/ QS=2QT= |
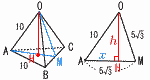 (1) 1辺の長さが10の正四面体の高さを求めよ。 (1) 1辺の長さが10の正四面体の高さを求めよ。【解】△OAMで考える h2=102-x2=(5 これを解いて,x= 高さh=√ {100-( 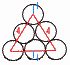 (2) 右図のように正三角柱の中に下の段から順に6個,3個,1個の半径1の球が互いに接するように積んである。最下段の6個の球はすべて正三角柱の底面と側面にも接している。また,最上段の球は正三角柱の上面に接している。この正三角柱の高さを求めよ。 (2) 右図のように正三角柱の中に下の段から順に6個,3個,1個の半径1の球が互いに接するように積んである。最下段の6個の球はすべて正三角柱の底面と側面にも接している。また,最上段の球は正三角柱の上面に接している。この正三角柱の高さを求めよ。【解】 高さ=(1辺4の正四面体の高さ)+(球の半径)×2 = |
||
| 2 | 須磨学園高校 (R7年) ★ | 5 | 中央大附属高校 (R7年) ★★ |
| 表面積が9πcm2である球の体積を求めなさい。 【解】 球の半径をrとすると,4πr2=9πより,r= 体積= |
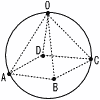 図のように,半径2の球が2つあり,それぞれが立方体の3つの面と接 し,2つの球が互いに外接している。立方体の1辺の長さを求めなさい。 図のように,半径2の球が2つあり,それぞれが立方体の3つの面と接 し,2つの球が互いに外接している。立方体の1辺の長さを求めなさい。【解】AP=BQ=√22+22+22=2 対角線AB=(2 1辺をxとすると,AB=√3x2= x=4+ |
||
| 3 | 中央大附属横浜高校 (R7年) ★★ | 6 | 桐蔭学園高校 (R6年) ★★ |
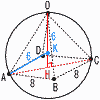 図のような半径5の半球形の容器と,底面の円の半径が3,高さが6の円錐形のおもりがある。半球形の容器には,水が満たされて水平な床に置いてある。容器の厚さは考えないものと して,(ただし,円周率はπとする。) 図のような半径5の半球形の容器と,底面の円の半径が3,高さが6の円錐形のおもりがある。半球形の容器には,水が満たされて水平な床に置いてある。容器の厚さは考えないものと して,(ただし,円周率はπとする。)(1) 容器に入った水の体積とおもりの体積の比を最も簡単な整数の比で答えなさい。 【解】半球= 円錐 (2) おもりの底面が床と常に平行になるように,おもりを容器の中に静かに入れていく。 次のようにおもりを入れたとき,あふれ出た水の体積を求めなさい。 ① おもりの底面を上側にして,最も深く入れたとき 【解】半径5/2,高さ5の円錐 水の体積= ② おもりの底面を下側にして,最も深く入れたとき 【解】上底半径1,下底半径3,高さ4の円錐台 水の体積=( |
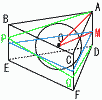 右の図のように,1辺の長さが4である正三角形を底面とする正三角柱ABC-DEFがある。この正三角柱のすぺての面に接する球Oがある。 右の図のように,1辺の長さが4である正三角形を底面とする正三角柱ABC-DEFがある。この正三角柱のすぺての面に接する球Oがある。(1) 球の半径は[ ]であり,正三角柱の体積は[ ]である。 【解】水平に2等分割するとき, 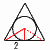 円Oは正三角形(1辺4)の内接円 円Oは正三角形(1辺4)の内接円半径=2÷ 体積=( (2) 球の中心をOとするとき,0A=[ ]である。 【解】OM=中線× OA=√ { ( 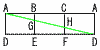 (3) 辺BE上に点G,辺CF上に点Hをとり,AG+GH+HDが最小になるときを考える。このとき,BG=[ ]である。 (3) 辺BE上に点G,辺CF上に点Hをとり,AG+GH+HDが最小になるときを考える。このとき,BG=[ ]である。【解】側面の展開図で考える BG= (4) (3)でとった点G,Hと点Aを通る平面でこの立体を切る。点Dを合むほうの立体の体積は[ ]である。 【解】立体は切頭三角柱(斜めにカット) 体積=(底面積)×(高さの平均) =4 |
||