| 30 正八面体 (略解) | ||
| 30 正八面体 (略解) | ||
| 1 | 法政大高校 (R7年) ★★ | 4 | 立教新座高校 (R7年) ★★★ |
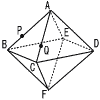 (1) 1辺の長さが12cmの立方体において,各面の対角線の交点を結んでできる右の図のような正八面体の体積を求めなさい。 (1) 1辺の長さが12cmの立方体において,各面の対角線の交点を結んでできる右の図のような正八面体の体積を求めなさい。【解】 中心を通る水平断面は,1辺6 体積= 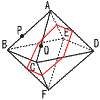 (2) (1)の正八面体において,各面の重心を頂点として結んでできる立体と元の正八面体の体積比を最も簡単な整数の比で表しなさい。 (2) (1)の正八面体において,各面の重心を頂点として結んでできる立体と元の正八面体の体積比を最も簡単な整数の比で表しなさい。【解】(1)の正八面体の平面図で考える 1辺4の立方体ができるから, 43:288=64:288=2:9 |
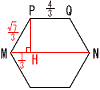 図1は,1辺の長さが6cmの正八面体の展開図です。図2は,図1の展開図を組み立ててできる正八面体です。 図1は,1辺の長さが6cmの正八面体の展開図です。図2は,図1の展開図を組み立ててできる正八面体です。ひもの長さが最も短くなるようにひもをかけるとき,辺 AJ上でひもがある位置をPとします。 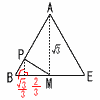 (1) ひもの長さを求めなさい。 (1) ひもの長さを求めなさい。【解】BF=√{(6+6+3)2+(3√3)2}=√252=6 (2) 図2の正八面体を3点B,H.Pを通る平面で切断したとき,切り口の図形の周の長さを 求めなさい。 【解】△BPJで,PJ=2より, BP2−52=22−12で, BP=2 切り口は1辺2 |
||
| 2 | 東京学芸大附属高校 (R5年) ★★ | 5 | 芝浦工大附属高校 (R7年) ★★ |
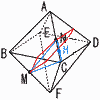 右の図のように,1辺の長さが2cmの正八面体ABCDEFがあり,辺BFの中点をM,辺ACの中点をNとする。 右の図のように,1辺の長さが2cmの正八面体ABCDEFがあり,辺BFの中点をM,辺ACの中点をNとする。(1) △ABFの面積を求めなさい。 【解】正方形ABFDの半分 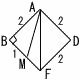 △ABF=22÷2=2cm2 △ABF=22÷2=2cm2(2) 線分AMの長さを求めなさい。 【解】△ABMは直角三角形 AM=√22+12= 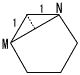 (3) 線分MNの長さを求めなさい。 (3) 線分MNの長さを求めなさい。【解】切り口は正六角形 MN= (4) △AMNの面積を求めなさい。 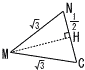 【解】△MNCは二等辺三角形 【解】△MNCは二等辺三角形MH=√(√3)2+(1/2)2= △AMN= |
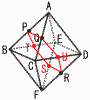 右の図のような,一辺の長さが1cmの正八面体において,辺AB,AC,DFの中点をそれぞれP,Q, Rとする。 3点P,Q,Rを含む平面でこの立体を切って2つに分けるとき, 右の図のような,一辺の長さが1cmの正八面体において,辺AB,AC,DFの中点をそれぞれP,Q, Rとする。 3点P,Q,Rを含む平面でこの立体を切って2つに分けるとき,(1) 頂点Aを含む立体の面の数を求めなさい。 【解】 正六角形1つ,台形3つ,正三角形4つの,計8つ (2) 切り口の面積を求めなさい。 【解】切り口は,1辺1/2の正六角形 面積= (3) 頂点Aを含む立体の表面積を求めなさい。 【解】(1)の8面の合計 ア 正六角形(1辺 イ 台形(上底 ウ 正三角形(1辺 エ 正三角形(1辺1)… ア+イ+ウ+エ= |
||
| 3 | 明治学院東村山高校 (R6年) ★★ | 6 | 鎌倉学園高校 (R6年) ★★ |
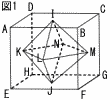 立方体に正八面体が接しています。また,図2はI,L,J,Nを通る平面で切断した断面です。 立方体に正八面体が接しています。また,図2はI,L,J,Nを通る平面で切断した断面です。(1) 立方体の1辺の長さが8cmのとき,正方形I LJNの1辺の長さを求めなさい。 【解】4 (2) 四角形KLMNの面積が32cm2のとき,立方体の1辺の長さを求めなさい。 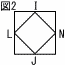 【解】KL=LJ=4 【解】KL=LJ=4(3) (2)のとき,正八面体の体積を求めなさい。 【解】(正四角錐I-KLMN)×2 正四角錐I-KLMNの高さIO= 体積=( |
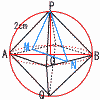 1辺が2cmである正八面体があります。 1辺が2cmである正八面体があります。(1) この正八面体に外接する球の半径を求めなさい。 【解】△OAPの等辺 半径=OA= 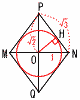 (2) この正八面体に内接する球の半径を求めなさい。 (2) この正八面体に内接する球の半径を求めなさい。【解】切断面PMQNで考える △ONH∽△PNO(3辺は1: 半径=OH=PO÷ |
||
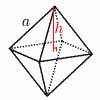 高 さ h= 体 積 V= 表面積S=2 |
|||