| 29 四面体 (略解) | ||
| 29 四面体 (略解) | ||
| 1 | 京都市立西京高校 (R6年) ★★★ | 4 | 埼玉県立高校 (R7年) ★ | |||
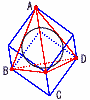 正四面体ABCDに半径1の球が内接している。この正四面体の1辺の長さを求めよ。ただし,内接するとは,球が正四面体のすべての面と接することである。 正四面体ABCDに半径1の球が内接している。この正四面体の1辺の長さを求めよ。ただし,内接するとは,球が正四面体のすべての面と接することである。【解】正四面体=立方体−三角錐×4 1辺aの正四面体= 半径1の球が内接する正四面体= ア=イより, |
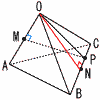 右の図のように,1辺の長さが6cmの正四面体 OABCの辺OB,OCの中点をそれぞれP,Qとします。 3点P,Q,Aを通る平面で正四面体OABCを切ったとき,頂点Bを含む立体の体積を求めなさい。 右の図のように,1辺の長さが6cmの正四面体 OABCの辺OB,OCの中点をそれぞれP,Qとします。 3点P,Q,Aを通る平面で正四面体OABCを切ったとき,頂点Bを含む立体の体積を求めなさい。【解】△OPQ∽△OBC(相似比1:2)
|
|||||
| 2 | 市川高校 (R5年) ★★★ | 5 | 大阪教育大附属高校 (R7年) ★★★ | |||
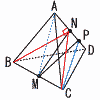
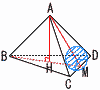 右の図のように,四面体ABCDがあり,AB=AC=AD=√21,CD=2√5,BC=BD=√30である。 右の図のように,四面体ABCDがあり,AB=AC=AD=√21,CD=2√5,BC=BD=√30である。また,CDの中点をM,Aから△BCDに下ろした垂線と△BCDとの交点をHとする。 (1) AMの長さを求めよ。 【解】△ACMで,AM=√(√25)2−(√5)2=4 (2) AHの長さを求めよ。 【解】 △BCMで,BM=√(√30)2−(√5)2=5 △ABMで,BH=xとすると, AH2=(√21)2−x2=42−(5−x)2で,x=3 AH2=(√21)2−32=12より, AH=√12=2 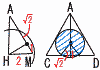 (3) Hを中心として半径 (3) Hを中心として半径【解】斜線部分=扇形+二等辺三角形 面積=( |
 AB=3,AC=2 AB=3,AC=2(1) 点Aから直線CDに垂線APを下ろすとき,線分PDの長さを求めなさい。 【解】△ADPで,∠D=60°より, PD=1 (2) 点Bから直線CDに垂線BQを下ろすとき,線分QDの長さを求めなさい。 【解】QD=xとすると,△BCDで,(3 18−16+8x−x2=10−x2より, QD=x=1 (PとQは一致) (3) △ABQの面積を求めなさい。 【解】△ABQ(等辺3,底辺 BM= (4) 四面体ABCDの体積を求めなさい。 【解】△ABQ⊥CD 体積= |
|||||
| 3 | 日本大第二高校 (R6年) ★★★ | 6 | ラ・サール高校 (R7年) ★★★ | |||
 図のように,1辺の長さが6の正四面体ABCDにおいて,2辺BC,ADの中点をそれぞれM,Nとし,辺AD上にAP=MPとなるような点Pをとる。 図のように,1辺の長さが6の正四面体ABCDにおいて,2辺BC,ADの中点をそれぞれM,Nとし,辺AD上にAP=MPとなるような点Pをとる。(1) 線分MNの長さを求めよ。 【解】MNは△NBCの中線 △NBCで,NB=NC=3 MN=√(3√32)−32=3 (2) 正四面体ABCDの体積を求めよ。 【解】△NBCは正四面体を,ADと垂直に2等分割している △NBC= 体積= (3) 四面体ABCPの体積を求めよ。 【解】(三角錐A-BNC)+(三角錐P-BNC) AP=xとすると,AP2=MP2=MN2+(AP−AN)2 x2=(3 体積= |
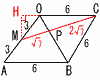 (1) 図1のように,1辺の長さが6の正方形ABCDを底面とし側面が正三角形である正四角すいと,点Pを頂点とする1辺の長さが6の正四面体を,正三角形の頂点どうしが重なるように斜線部分の面で貼り合わせる。このとき,頂点Pから底面ABCDを含む平面に下ろした垂線の長さを求めよ。 (1) 図1のように,1辺の長さが6の正方形ABCDを底面とし側面が正三角形である正四角すいと,点Pを頂点とする1辺の長さが6の正四面体を,正三角形の頂点どうしが重なるように斜線部分の面で貼り合わせる。このとき,頂点Pから底面ABCDを含む平面に下ろした垂線の長さを求めよ。【解】対称面OECPで考える △PFHで,PH=√(3√3)2−32=3 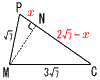 (2) 図2のように,1辺の長さが6である2つの正四面体を(1)と同じように斜線部分の面で貼り合わせる。このとき,頂点Pから三角形ABCを含む平面に下ろした垂線の長さを求めよ。 (2) 図2のように,1辺の長さが6である2つの正四面体を(1)と同じように斜線部分の面で貼り合わせる。このとき,頂点Pから三角形ABCを含む平面に下ろした垂線の長さを求めよ。【解】(1)と同様,対称面で考える ON=3 (3 AM=√(3√3)2−(√3)2=2 PH=AP×(MN/AN)= |
|||||
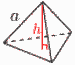 高 さ h= 表面積S= |
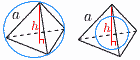 外接球の半径R= 内接球の半径r= |
|||||