| 31 動点3 (解答) | ||
| 31 動点3 (解答) | ||
| 1 | 和歌山県立高校 (R6年) ★ | 4 | 駿台甲府高校 (R7年) ★★ |
||||||||||||||||||||
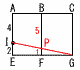
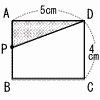 右の図のような長方形ABCDがある。点Pは点Aを出発して長方形の辺上をB,Cの順にCまで動くものとし,点Pが点Aからxcm動いたときの△APDの面積をycm2とする。 右の図のような長方形ABCDがある。点Pは点Aを出発して長方形の辺上をB,Cの順にCまで動くものとし,点Pが点Aからxcm動いたときの△APDの面積をycm2とする。【解】 ア ・PがAB上(0≦x≦4)のとき, y= ・PがBC上(4≦x≦9)のとき,y= 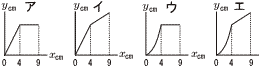 |
 右図のような,1辺10cmの正三角形ABCにおいて,点PはAを出発レて,辺AB上を毎秒2cmで動き,点QはCを出発して,辺CA上を毎秒1cmで動く。2点P,Qは同時に出発し5秒間動くとき,△APQの面積が10 右図のような,1辺10cmの正三角形ABCにおいて,点PはAを出発レて,辺AB上を毎秒2cmで動き,点QはCを出発して,辺CA上を毎秒1cmで動く。2点P,Qは同時に出発し5秒間動くとき,△APQの面積が10【解】x秒後とすると, AP=2x AQ=10-x
|
||||||||||||||||||||||
| 2 | 大阪教育大附属池田校舎 (R5年) ★★ | 5 | 埼玉県立高校 (R5年) ★★★ | ||||||||||||||||||||
| AB=4cm,BC=3cm,∠B=90゜の直角三角形ABCがある。 (1) xの変域が次のとき,yをxの式で表しなさい。 【解】 ① 0≦x≦4(QはAC上) y= ② 4≦x≦5(QはAC上) y= ③ 5≦x≦8(QはCB上) y= 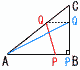 (2)△APQ= (2)△APQ=【解】△APQ= (1)の解に代入して,①より,x=√5 ②より,x= (3) tの値と△APQの面積を求めなさい。 【解】t秒後は①,t+3秒後は③ △APQ= |
 1辺4cmの正方形を底面とし,高さが6cmの直方体ABCD-EFGHがあり,辺AE上に,AI=4cmとなる点I をとります。 1辺4cmの正方形を底面とし,高さが6cmの直方体ABCD-EFGHがあり,辺AE上に,AI=4cmとなる点I をとります。(1) IP+PGの長さが最も短くなるのは,点Pが頂点Bを出発してから何秒後か求めなさい。 【解】展開図参照 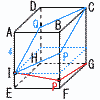 BP=5より, 5秒後 BP=5より, 5秒後(2) できる2つの立体のうち,頂点Aを含む立体の体積 【解】(青線図)1辺4cmの立方体× 体積=43× (3) x秒後の△I PQは,球とちょうど1点で接しました。xの値を求 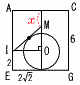 めなさい。 めなさい。【解】切断面AEGCで考える PQの中点をM,BP=xとすると, x+2√2+2=6より, x=4-2√2 |
||||||||||||||||||||||
| 3 | 市立西京高校 (R6年) ★★ | 6 | 東京科学大科技高校 (R7年) ★★★ | ||||||||||||||||||||
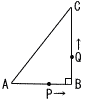 図のように,AB=8cm,,BC=12cmの直角三角形ABCがある。点Pは点Aを出発し,A→B→Cの順に毎秒2cmの速さで辺上を移動し,点Qは点Pが点Aを出発すると同時に点Bを出発し,B→Cの順に毎秒1cmの速さで辺上を移動する。点P,点Qのどちらかが先に点Cに着いたとき,点P,点Qはともに停止する。 図のように,AB=8cm,,BC=12cmの直角三角形ABCがある。点Pは点Aを出発し,A→B→Cの順に毎秒2cmの速さで辺上を移動し,点Qは点Pが点Aを出発すると同時に点Bを出発し,B→Cの順に毎秒1cmの速さで辺上を移動する。点P,点Qのどちらかが先に点Cに着いたとき,点P,点Qはともに停止する。(1) 線分PQが辺ACと平行になるときの△APQの面積を求めよ。 【解】BP:BQ=8:12=2:3となればよい x秒後とすると,(8-2x):x=2:3で,x=3 △APQ= (2) 点Pが点Aを出発してからx秒後に△APQの面積が2cm2となる。xの値をすべて求めよ。 【解】 ・PがAB上(0≦x≦4)のとき, ・PがBC上(4≦x≦10)のとき,PQ=x-(2x-8)=8-x ・PがC上(10≦x≦12)のとき,PQ=12-x |
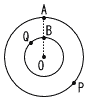
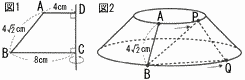 図1の台形ABCDを辺CDを軸として回転させてできる図2の立体がある。この立体について,点PはAを出発して,円の周上を一定の速さで動き続け,24秒ごとにAを通過する。点QはPと同時にBを出発して,円の周上を一定の速さでPと同じ向きに動き続け,48秒ごとにBを通過する。 図1の台形ABCDを辺CDを軸として回転させてできる図2の立体がある。この立体について,点PはAを出発して,円の周上を一定の速さで動き続け,24秒ごとにAを通過する。点QはPと同時にBを出発して,円の周上を一定の速さでPと同じ向きに動き続け,48秒ごとにBを通過する。【解】円すい台=大円すい× ( (2) 点Pが出発してから12秒後の線分BPの長さを求めなさい。 【解】Pは,Aの180°反対側 BP=√122+42=4 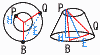 (3) 2点P,Qが出発してから64秒後の△PBQの面積を求めなさい。 (3) 2点P,Qが出発してから64秒後の△PBQの面積を求めなさい。【解】Pは2 △PEHで,PH=4,EH=8より,PE=4 △PBQ= |
||||||||||||||||||||||