 関数 |
９ 二乗に比例 （略解） | |
| １ | 山口県立高校 （Ｒ７年） ★ | ４ | 広島県立高校 （Ｒ６年） ★ | |||||||
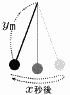 1往復するのにx秒かかるふりこの長さをyｍとすると,xとyの間には,y＝ x2という関係がある。1往復するのに6秒かかるふりこの長さは何ｍか求めなさい。【解】 y＝ x2にx＝6を代入して, y＝×62＝9m |
yはxの2乗に比例し,x＝6のときy＝12です。このとき,yをxの式で表しなさい。 【解】 y＝ax2に(6,12)を代入して,62a＝12で, a＝  よって, y＝  x2 |
|||||||||
| ２ | 京都府立高校 （Ｒ６年） ★★ | ５ | 筑波大附属坂戸高校 （Ｒ５年） ★ | |||||||
| yはxの2乗に比例し,x＝3のときy＝－54である。このとき,yをxの式で表せ。 【解】 y＝ax2に(3,－54)を代入して,32a＝－54で, a＝－6 よって, y＝－6x2 |
yはxの2乗に比例し,x＝3のときy＝27です。yをxの式で表しなさい 【解】 y＝ax2に(3,27)を代入して,32a＝27で, a＝3 よって, y＝3x2 |
|||||||||
| ３ | 専修大附属高校 （Ｒ６年） ★★ | ６ | 愛媛県立高校 （Ｒ６年） ★ | |||||||
| 車の運転において,運転手が危険を感じてからブレーキをかけ,実際に車が停止するまでの距離を停止距離という。停止距離は次の2つの距離の和である。 ①空走距離 運転手が危険を感じてからブレーキがきき始めるまでに車が進む距離のことで,車の速さに比例する。 (例) 時速20kmで走行したときの空走距離が6mの場合,2倍の速さ(時速40km)で走行したときの走行距離は6×2＝12より12mとなる。 ②制動距離 ブレーキがきき始めてから実際に車が停止するまでに進む距離のことで,車の速さの2乗に比例する。[2乗に比例する]とは速さが2倍こなると制動距離は4倍に,速さが3倍になると制動距離は9倍になるということである。 (例) 時速20kmで走行したときの制動距離が3mの場合,2倍の速さ(時速40km)で走行したときの制動距離は3×22＝3×4＝12より12mとなる。 したがって,①②の例の場合,時速20kmで走行したときの停止距離は6＋3＝9より9m,時速40kmで走行したときの停止距離は12＋12＝24より24mとなる。 時速20 mで走行したときの空走距離が6ｍ,制動距離が3ｍとして,次の各問いに答えなさい。なお,答えが小数となった場合は,小数第１位を四捨五入し,整数で答えなさい。 (1) 時速50kmで走行したときの場合の停止距離 【解】50÷20＝2.5倍だから, 停止距離＝6×2.5＋3×2.52＝15＋18.25≒34m (2) 時速20kmのx倍の速さのときの停止距離をxを用いて表しなさい。 【解】 停止距離＝6×x＋3×x2＝3x2＋6x (右へつづく→) |
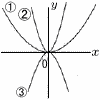 図において,放物線①,②,③はそれぞれ関数y＝ax2,y＝bx2,y＝cx2のグラフである。a,b,cを,値の小さい順に左から並べて書け。【解】 c, a, b |
|||||||||
| ７ | 慶應義塾志木高校 （Ｒ６年） ★★★ | |||||||||
| 登山地図などに書かれているコースの歩行時間を「コースタイム」という。傾斜率s(s≧0)の斜面を登るとき,距離dkmのコースタイムTは，定数a,b,cを用いてT＝{(as2 ＋bs＋c)×d}分と算出されるとする。傾斜率0で距離2kmのコースタイムは40分,傾斜率0.1で距離1kmのコースタイムは26.5分,傾斜率0.2で距離1kmのコースタイムは36分となる。
(1）定数a,b,cの値を求めよ。 【解】
（2）傾斜率sで距離9kmのコースタイムが324分であるとき,sの値を求めよ。 【解】 324=(150s2＋50s＋20)×9 (5s－1)(15s＋8)＝0で,s＞0だから, s＝0.2 |
||||||||||
| (3) 停止距離が72mとなるとき,車の速さは時速何kｍか 【解】 3x2＋6x＝72より,(x－4)(x＋6)＝0で,x＝4倍 速さ＝20×4＝80km/時 |
||||||||||
