 関数 |
３ 一次関数１ （略解） | |
| １ | 市立福山高校 （Ｒ７年） ★ | ５ | 桜美林高校 （Ｒ５年） ★ | ||||||||||||||||||
| 2点(－2,1), (1,3)を通る直線の式を求めなさい。 【解】
|
点A(－2,10), B(4,－6), C(－5,k) が 一直線上のとき,kの値 【解】ABの傾き＝ACの傾き
|
||||||||||||||||||||
| ２ | 奈良大附属高校 （Ｒ７年） ★★ | ６ | 高知県立高校 （Ｒ７年） ★ | ||||||||||||||||||
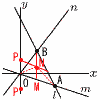 右の図のように,3直線 l：2x＋y＝10, m：x＋3y＝0, n：4x－3y＝0がある。 l とmの交点をA,l とnの交点をBとするとき,⑴ 点Aの座標を求めなさい。
⑶ △OAPの面積が,△OABの面積の半分となるようなy軸上の点P の座標をすべて求めなさい。 【解】底辺OAは共通 高さMN＝  MB＝ になればよいよって, P(0,  ) P(0,－) |
関数y＝－2x＋6 のグラフについて述べた文として正しいものを,次のア～エからすべて選び,その記号を書きなさい。 ア xの値が増加すると,yの値は減少する。 イ 点(－2,6)を通る直線である。 ウ グラフの傾きは6である。 エ 方程式2x＋y－6＝0のグラフと一致する 【解】ア エ |
||||||||||||||||||||
| ７ | 宇都宮短大附属高校 （Ｒ７年） ★ | ||||||||||||||||||||
あるばねにおもりをつるすとき,このばねの伸びる長さはおもりの重さに比例する｡下の表は様々な重さのおもりをばねにつるしてばね全体の艮さを調べたものである。ばね全体の長さが23cmになるのは[ ]ｇのおりをつるすときである。
表より,4gで2cm伸びる y＝ x＋8にy＝23を代入して,23＝ x＋8より, x＝30ｇ |
|||||||||||||||||||||
| ３ | 明治学院高校 （Ｒ５年） ★★ | ８ | 大阪教育大附属平野校舎 （Ｒ５年） ★ | ||||||||||||||||||
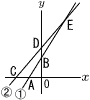 (1) △AOBの面積をsを用いて表せ。【解】A(－  s,0) B(0,s)△AOB＝ ×s×s＝ s2 …ア(2) 点Eのx座標を.s,tを用いて表せ。 【解】  x＋s＝ x＋tより,(－)x＝t－sで, x＝ (t－s)(3) s＝3で,△AECと△ODCの面積が等しいとき,tの値を求めよ。 【解】重なる□ABDCを引くと,△EDB＝△AOB △EDB＝ (t－3)× (t－3)＝ (t－3)2 …イア＝イより,  ×32＝(t－3)2で, t＝3±t＞s＝3だから, t＝  |
(1) k＜b＜k＋1 【解】切片bは,0と1の間 (0＜b＜1) 0＜b＜0＋1で, k＝0 (2) l＜a＜l＋1 【解】傾きaは,アとイの間(－2＜a＜－1) 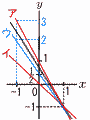 －2＜a＜－2＋1で, l＝－2(3) a＋b＝m 【解】x＝1のとき,y＝a＋b＝m (1,－1)を通るから, y＝m＝－1 (4) n＜－a＋b＜n＋1 【解】x＝－1のとき,y＝－a＋b＝n アとウの間,つまり(－1,2)と(－1,3)の間で, x＝－1のとき,2＜y＜3より,2＜n＜3 2＜－a＋b＜2＋1で, n＝2 |
||||||||||||||||||||
| ４ | 愛媛県立高校 （Ｒ６年） ★ | ９ | 西大和学園高校 （Ｒ６年） ★★★ | ||||||||||||||||||
 図は,1辺に4個の碁石を並べた正五角形で,並べた碁石は全部で15個である。1辺にn個の碁石を並べた正五角形をつくったとき,並ぺた碁石は全部で何個か,nを使って表せ。ただし,nは2以上の自然数とする。【解】(右図参照) 5((n－1)＝(5n－5)個 |
直線4x＋5y＝2…ア, ax＋3y＝0…イ の交点をPとし,直線－x＋2y＝7…ウ, 5x＋by＝－1…エ の交点をQとすると,P,Qは原点に関して対称になった。このとき,a,bの値を求めよ。 【解】原点対称だから,P(c,b)とすると,Q(－c,－d) アにPを代入すると,4c＋5d＝2 …オ ウにQを代入すると,－(－c)＋2(－d)＝7…カ オカを連立させて解くと,c＝3,d＝－2 これらをイエに代入して, a＝2, b＝7 |
||||||||||||||||||||
