| �P�@���Ɣ�����P�@�i�����j | ||
| �P�@���Ɣ�����P�@�i�����j | ||
| �P | ���쌧�����Z�@�i�q�T�N�j�@�� | �T | �X�������Z�@�i�q�V�N�j�@�� | ||||||||
�@12m�̃��[�v��x���������Ƃ���,1�{���̃��[�v�̒�����ym�Ƃ���Bx��y�̊W�ɂ��Ă����邱�Ƃ�,2�I�я����Ȃ����B
�y���z�����͖{���ɔ���Ⴗ�� y��12/x����, �C�@�@xy��12����, �E |
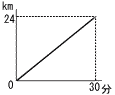 �@�Ƃ���24km���ꂽ�}���ق�,�����Ԃň��̑����Ō��������B�E�̐}��,�o�����Ă���x����̉Ƃ���̓��̂��ykm�Ƃ���,�}���قɒ����܂ł�x��y�̊W��\�����O���t�ł���B�Ƃ���18km�̒n�_��ʉ߂����̂�,�Ƃ��o�����Ă��牽�����b�ォ,���߂Ȃ����B �@�Ƃ���24km���ꂽ�}���ق�,�����Ԃň��̑����Ō��������B�E�̐}��,�o�����Ă���x����̉Ƃ���̓��̂��ykm�Ƃ���,�}���قɒ����܂ł�x��y�̊W��\�����O���t�ł���B�Ƃ���18km�̒n�_��ʉ߂����̂�,�Ƃ��o�����Ă��牽�����b�ォ,���߂Ȃ����B�y���z �����͎��Ԃɔ�Ⴗ�邩��, �@x:30��18:24���, �@x��18�~30��24��22.5��22��30�b�� �@ |
||||||||||
| �Q | ����t�����썂�Z�@�i�q�V�N�j�@���� | �U | �v���đ啍�ݍ��Z�@�i�q�T�N�j�@���� | ||||||||
| �@y�|2��x�{1�ɔ�Ⴕ,z��y�ɔ���Ⴕ,x��2�̂Ƃ�y��8�Cz��1�ƂȂ�܂��Bz��6�̂Ƃ�,x�̒l�����߂Ȃ����B �y���z y�|2��a(x�{1)��(2,8)�������āC6��3a �@a��2��,y��2(x�{1)�{2��2x�{4�c�A z��\(\frac{b}{y}\)��(8,1)��������,1��\(\frac{b}{8}\) �@b��8�ŁCz��\(\frac{8}{y}\)�c�C �C��z��6���������,y��\(\frac86\)��\(\frac43\) �@������A�ɑ�������,\(\frac43\)��2x�{4���, x��\(\color{red}{\frac43}\) |
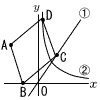 �@y�� �@y���y���zAB D(k,6/k)�Ƃ����, C(k�{ C���@�ɑ������, 6/k�| �@(3k�|2)(k�{6)��0��, k��0������, k�� �����, D( |
||||||||||
| �R | �R�`�������Z�@�i�q�T�N�j�@�� | �V | �����吙�����Z�@�i�q�U�N�j�@���� | ||||||||
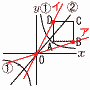 �@�E�̐}�ɂ�����,�@�͊�y�� �@�E�̐}�ɂ�����,�@�͊�y��(1) a�̒l�����߂Ȃ����B �y���zA�̍��W���@�ɑ�� AB��BC��4,B(7,2)���, A(3,2) �����y�� (2) ��y��bx�̃O���t���l�p�`ABCD�̕ӏ�̓_��ʂ�Ƃ�,b�̂Ƃ�l�͈̔͂�,�s�������g���ĕ\���Ȃ����B �y���z�A�͌��_O��ʂ钼����,b�͂��̌X�� B(7,2)���,�A����OB�̌X���� D(3,6)���,�C����OD�̌X����2 �����, |
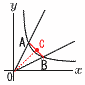 �@�}�ɂ����ē_�`��y�� �@�}�ɂ����ē_�`��y��(1) �_�`�̍��W�����߂Ȃ����B �y���z (2) �_C��x���W�����߂Ȃ����B �y���z C��x���W��, ( (3) ����OC�̒��������߂Ȃ����B �y���zC( OC�����@{( (4) ��O�`�a�̖ʐς����߂Ȃ����B �y���z���AB��1, ����OC�� ��O�`�a�� �@ |
||||||||||
| �S | �����啍�����l���Z�@�i�q�U�N�j�@�� | ||||||||||
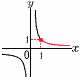 �@��y�� �@��y�� �A y��1�@�C y��1�@�E 0��y��1�@�G 0��y��1�@�I �|1��y�� 1 �y���z(�E��}�Q��) �E |
|||||||||||